The divideandaverage method, dating back to the Babylonians, ca. 1700 B.C., can be used to approximate the square root of any positive number A. We will look at this method here.

Let A be the number whose square root is sought. After assigning a first guess of x0 for the square root of A, the method repeatedly divides A by the current guess, xi, and then averages the quotient with xi. The average is the new guess. This is repeated until the square root is approximated to the desired accuracy. The iterative formula for this method is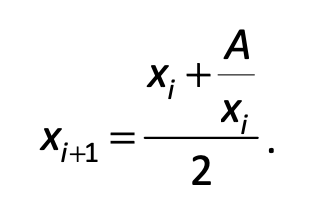

Consider an example of the divideandaverage method. Suppose we want to calculate the square root of 2. We take a guess as 1.5 and then proceed with the iterations.

The first iteration gives (1.5+2/1.5)/2 = 1.41666666666.

The second iteration gives (1.41666666666+2/1.41666666666)/2 = 1.41421568628.

Since the square root of 2 is 1.41421356237, the algorithm is doing rather well.

Complete the statements below in a MATLAB function file named SquareRoot.m to have it estimate the value of a square root.

function [fx,ea,iter] = SquareRoot(A,es,maxit) % Divide and average method for evaluating square roots % [fx,ea,iter] = SquareRoot(A,es,maxit) % Input: % A = value for which square root is to be computed % es = stopping criterion (default = 0.0001) % maxit = maximum iterations (default = 50) % Output: % fx = estimated value % ea = approximate relative error (%) % iter = number of iterations % Defaults: if nargin=maxit, break, end end fx = sol; end

Verify the execution your SquareRoot function by entering these statements in the command window:

>> format long >> [fx,ea,iter] = SquareRoot(2,.001,3) >> [fx,ea,iter] = SquareRoot(2,.001,10) >> [fx,ea,iter] = SquareRoot(2) 

What do you observe for the output of the SquareRoot function given the input parameters above and the function's various means for terminating the iterations?

xi+1=2xi+xiA