The easiest way to understand kinematics is by developing it on a $2$D robotic arm that contains two links, two joints and one end$-$effector or a gripper. The first

joint will rotate, but it is connected to a table or the floor by a foundation. While link $11$ connects it to a second joint that can translate and rotate, a second link $12$

links this joint to the fixed$-$end effector.

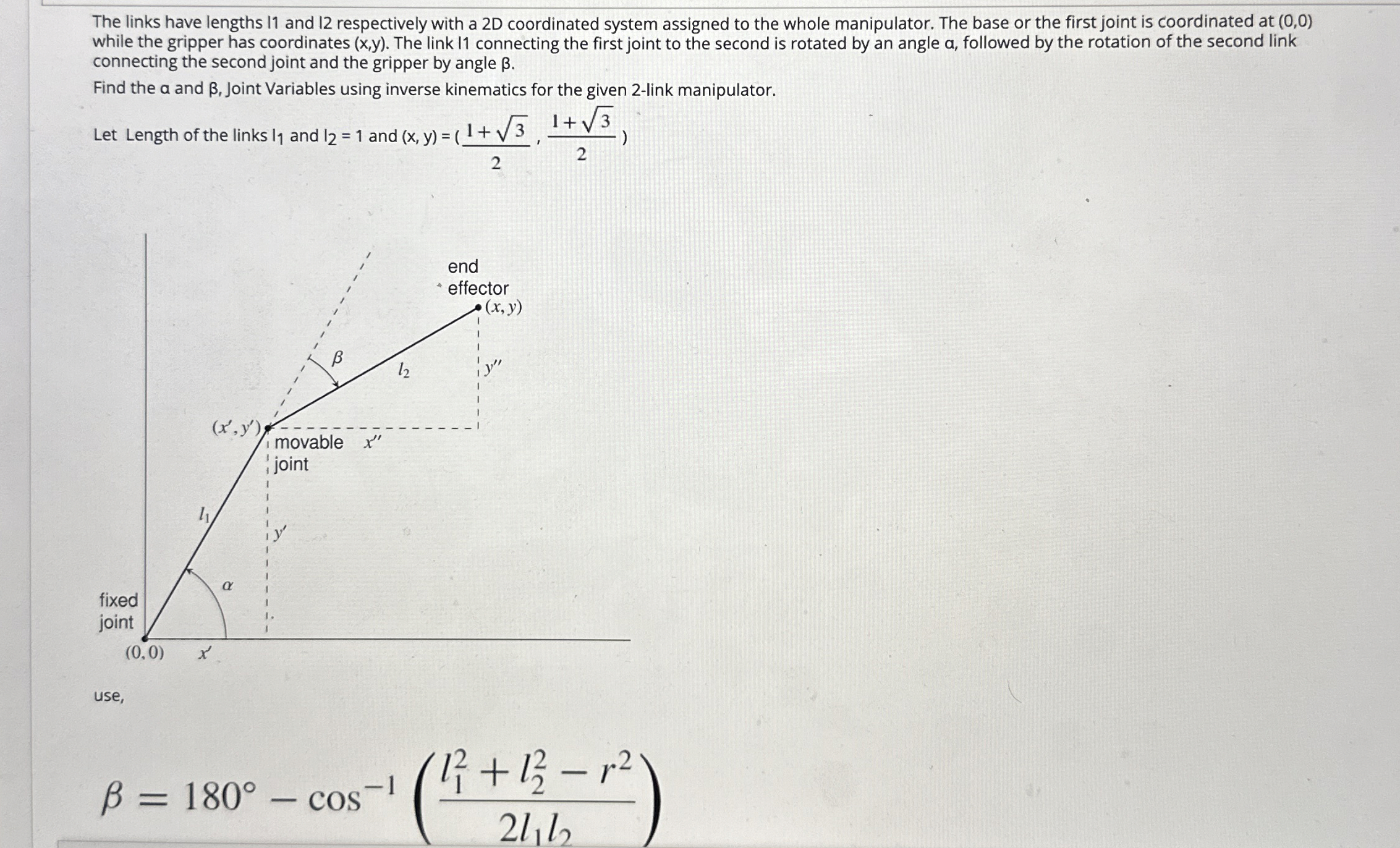
The links have lengths $I1$ and $I2$ respectively with a $2$D coordinated system assigned to the whole manipulator. The base or the first joint is coordinated at $(0,0)$

while the gripper has coordinates $(x,y).$ The link II connecting the first joint to the second is rotated by an angle a$,$ followed by the rotation of the second link

connecting the second joint and the gripper by angle $.$

Find the a and $,$ Joint Variables using inverse kinematics for the given $2-$link manipulator.

Let Length of the links $I_1$ and $I_2=1$ and $(x,y)=(\frac{1+\sqrt[\phantom{2}]{3}}{2},\frac{1+\sqrt[\phantom{2}]{3}}{2})$

$=180-co{s}^{-1}(\frac{l_1^2+l_2^2-r^2}{2l_1{l}_2})$

The links have lengths $I1$ and $I2$ respectively with a $2$D coordinated system assigned to the whole manipulator. The base or the first joint is coordinated at $(0,0)$

while the gripper has coordinates $(x,y).$ The link $11$ connecting the first joint to the second is rotated by an angle $a,$ followed by the rotation of the second link

connecting the second joint and the gripper by angle $.$

Find the a and $,$ Joint Variables using inverse kinematics for the given $2-$link manipulator.

Let Length of the links $I_1$ and $I_2=1$ and $)$

use,

$=180-co{s}^{-1}(\frac{l_1^2+l_2^2-r^2}{2l_1{l}_2})$