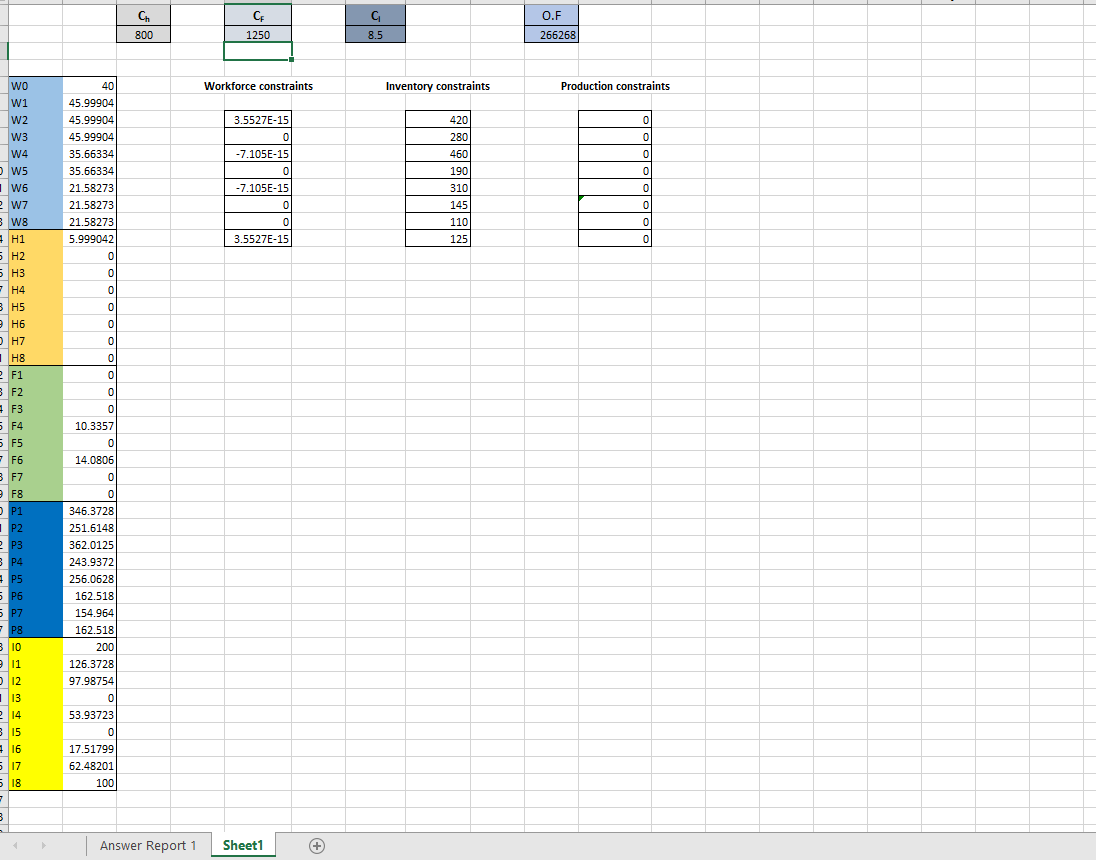
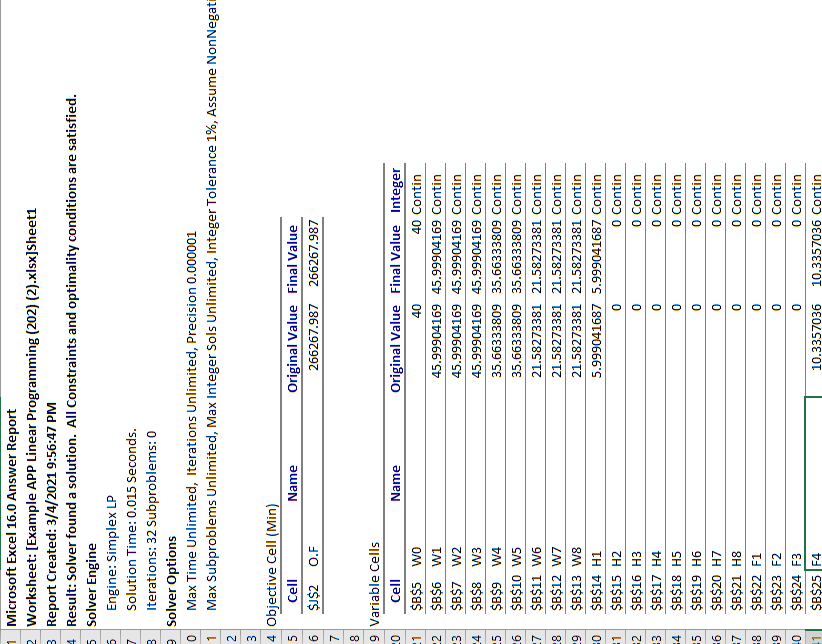
the excel file provide the data and final solution

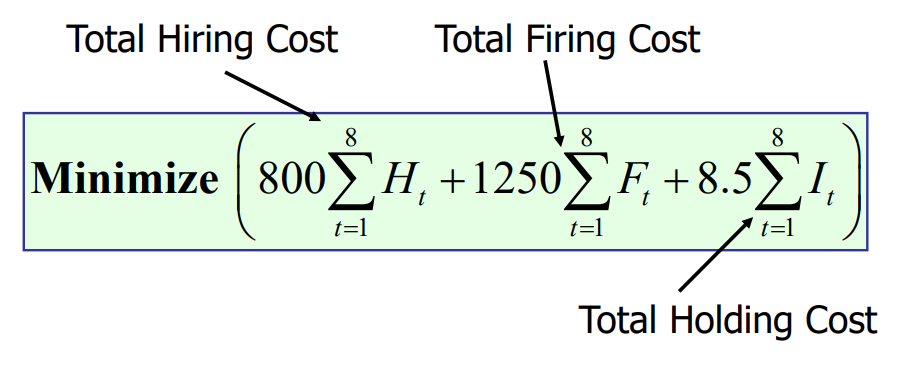
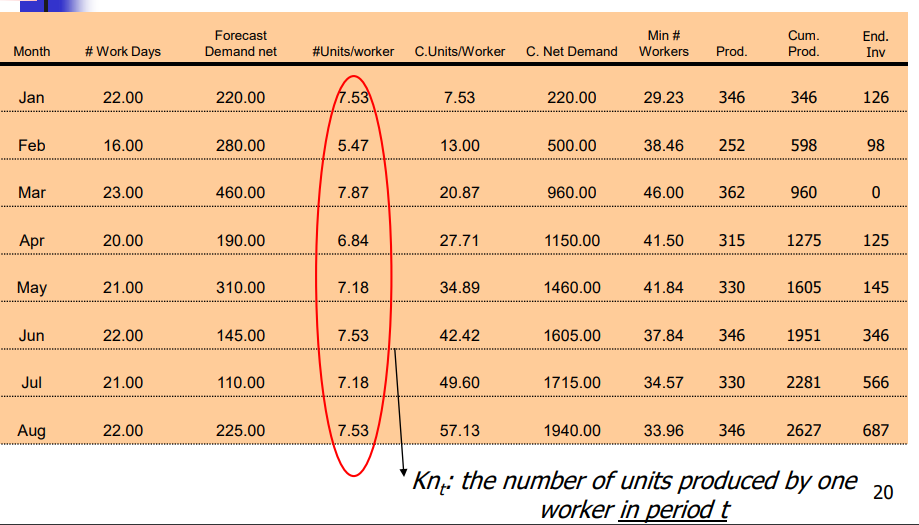
solve this optimization problem by using another software not excel

you may use Lingo

Ch 800 CE 1250 8.5 O.F 266268 Workforce constraints Inventory constraints Production constraints 0 0 0 40 45.99904 45.99904 45.99904 35.66334 35.66334 21.58273 21.58273 21.58273 5.999042 0 0 0 0 0 3.5527E-15 -7.105E-15 0 -7.105E-15 0 0 420 280 460 190 310 145 110 125 0 0 0 0 3.5527E-15 wo W1 W2 W3 W4 W5 W6 2 W7 B W8 # H1 5 H2 5 H3 - H4 3 H5 H6 H7 H8 2 F1 BF2 # F3 5 F4 5 F5 - F6 3 3 F7 F8 P1 1 P2 P3 3 P4 4 P5 5 P6 5 5 P7 7 P8 310 9 11 12 | 13 214 3 B 15 16 5 17 518 - 0 0 0 0 10.3357 0 14.0806 0 0 346.3728 251.6148 362.0125 243.9372| 256.0628 162.518 154.964 162.518 200 126.3728 97.98754 0 53.93723 0 17.51799 62.48201 100 3 Answer Report 1 Sheet1 + 3 1 Microsoft Excel 16.0 Answer Report 2 Worksheet: [Example APP Linear Programming (202) (2).xlsx]Sheet1 3 Report Created: 3/4/2021 9:56:47 PM 4 Result: Solver found a solution. All Constraints and optimality conditions are satisfied. 5 Solver Engine Engine: Simplex LP Solution Time: 0.015 Seconds. Iterations: 32 Subproblems: 0 Solver Options 0 Max Time Unlimited, Iterations Unlimited, Precision 0.000001 1 Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 1%, Assume NonNegati 7 3 2 3 4 Objective Cell (Min) Cell Name 6 $J$2 O.F Original Value Final Value 266267.987 266267.987 Name in On 0 minon a on min on 0 ao 8 9 Variable Cells 10 Cell 1 $B$5 WO -2 $B$6 W1 -3 $B$7 W2 4 $B$8 W3 5 $B$9 W4 6 $B$10 W5 $B$11 W6 18 $B$12 W7 9 $B$13 W8 0 $B$14 H1 1 $B$15 H2 2 $B$16 H3 $B$17 H4 $B$18 H5 : $B$19 H6 $B$20 H7 :7 $B$21 H8 8 $B$22 F1 9 $B$23 F2 $B$24 F3 1 $B$25 F4 Original Value Final Value Integer 40 40 Contin 45. 904169 45.99904169 Contin 45.99904169 45.99904169 Contin 45.99904169 45.99904169 Contin 35.66333809 35.66333809 Contin 35.66333809 35.66333809 Contin 21.58273381 21.58273381 Contin 21.58273381 21.58273381 Contin 21.58273381 21.58273381 Contin 5.999041687 5.999041687 Contin 0 0 Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 10.3357036 10.3357036 Contin Employee Constraints: W, -W-1 -H, +F, = 0 Specifically: W -W. -H, +F = 0 : W -W, - H2 +Fx = 0 Inventory Constraints: P,-1, +1+1+S, = D, specifically: P-1, +1, +S = D. 1: P-1, +1, +Sg =D Production Constraints: P. - kn,W, -0, +U, = 0 specifically: P - knW, -0, +U, = 0 Pg kngW-0+Ug = 0 Finally, we need constraints defining: . Initial Workforce size: Wo . Starting Inventory: 1 . Final Desired Inventory: Ig And, of course, the general constraint forcing all variables to be > 0 Total Hiring Cost Total Firing Cost 8 8 8 Minimize 800, +1250 + 8.5, t=1 t=1 t=1 Total Holding Cost Employee Constraints: W -W. -H, +F = 0, W -W, -H2 +F2 = 0, W-W-Hz +F3 = 0, W4-W-H4 +F4 = 0, W-W. -H, +F, = 0, W. -W5 - H6 +F6 = 0, W-W. -H, +F, = 0, W -W. - He + Fg = 0; Inventory Constraints: + + P. -1, +1. = 420 P2 12 +11 = 280 P2 13 +12 = 460 P,-1+1] = 190 P - 13 + 14 = 310 P-16 +1; = 145 P,-1, +1, -110 P-12 +1, =125 Production Constraints: P, kn,W, -0, +U, = 0 specifically: P. - kn,W- 0, +U, = 0) Po knW 0+Ug = 0 Month #Work Days Forecast Demand net Min # Workers Cum. Prod. C.Units/Worker C. Net Demand End. Inv #Units/worker Prod. Jan 22.00 220.00 17.53 7.53 220.00 29.23 346 346 126 Feb 16.00 280.00 5.47 13.00 500.00 38.46 252 598 98 Mar 23.00 460.00 7.87 20.87 960.00 46.00 362 960 0 Apr 20.00 190.00 6.84 27.71 1150.00 41.50 315 1275 125 May 21.00 310.00 7.18 34.89 1460.00 41.84 330 1605 145 Jun 22.00 145.00 7.53 42.42 1605.00 37.84 346 1951 346 Jul 21.00 110.00 7.18 49.60 1715.00 34.57 330 2281 566 Aug 22.00 225.00 7.53 57.13 1940.00 33.96 346 2627 687 Knt: the number of units produced by one worker in period t 20 Production levels Constraints: P. 7.53W, = 0 P2-5,47W = 0 Pz 7.87W2 = 0 P4 -6.84W, = 0 P3 7.18W, = 0 P-7.53W = 0 P. 7.18W, = 0 P - 7.53W, = 0 Ch 800 CE 1250 8.5 O.F 266268 Workforce constraints Inventory constraints Production constraints 0 0 0 40 45.99904 45.99904 45.99904 35.66334 35.66334 21.58273 21.58273 21.58273 5.999042 0 0 0 0 0 3.5527E-15 -7.105E-15 0 -7.105E-15 0 0 420 280 460 190 310 145 110 125 0 0 0 0 3.5527E-15 wo W1 W2 W3 W4 W5 W6 2 W7 B W8 # H1 5 H2 5 H3 - H4 3 H5 H6 H7 H8 2 F1 BF2 # F3 5 F4 5 F5 - F6 3 3 F7 F8 P1 1 P2 P3 3 P4 4 P5 5 P6 5 5 P7 7 P8 310 9 11 12 | 13 214 3 B 15 16 5 17 518 - 0 0 0 0 10.3357 0 14.0806 0 0 346.3728 251.6148 362.0125 243.9372| 256.0628 162.518 154.964 162.518 200 126.3728 97.98754 0 53.93723 0 17.51799 62.48201 100 3 Answer Report 1 Sheet1 + 3 1 Microsoft Excel 16.0 Answer Report 2 Worksheet: [Example APP Linear Programming (202) (2).xlsx]Sheet1 3 Report Created: 3/4/2021 9:56:47 PM 4 Result: Solver found a solution. All Constraints and optimality conditions are satisfied. 5 Solver Engine Engine: Simplex LP Solution Time: 0.015 Seconds. Iterations: 32 Subproblems: 0 Solver Options 0 Max Time Unlimited, Iterations Unlimited, Precision 0.000001 1 Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 1%, Assume NonNegati 7 3 2 3 4 Objective Cell (Min) Cell Name 6 $J$2 O.F Original Value Final Value 266267.987 266267.987 Name in On 0 minon a on min on 0 ao 8 9 Variable Cells 10 Cell 1 $B$5 WO -2 $B$6 W1 -3 $B$7 W2 4 $B$8 W3 5 $B$9 W4 6 $B$10 W5 $B$11 W6 18 $B$12 W7 9 $B$13 W8 0 $B$14 H1 1 $B$15 H2 2 $B$16 H3 $B$17 H4 $B$18 H5 : $B$19 H6 $B$20 H7 :7 $B$21 H8 8 $B$22 F1 9 $B$23 F2 $B$24 F3 1 $B$25 F4 Original Value Final Value Integer 40 40 Contin 45. 904169 45.99904169 Contin 45.99904169 45.99904169 Contin 45.99904169 45.99904169 Contin 35.66333809 35.66333809 Contin 35.66333809 35.66333809 Contin 21.58273381 21.58273381 Contin 21.58273381 21.58273381 Contin 21.58273381 21.58273381 Contin 5.999041687 5.999041687 Contin 0 0 Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 0 O Contin 10.3357036 10.3357036 Contin Employee Constraints: W, -W-1 -H, +F, = 0 Specifically: W -W. -H, +F = 0 : W -W, - H2 +Fx = 0 Inventory Constraints: P,-1, +1+1+S, = D, specifically: P-1, +1, +S = D. 1: P-1, +1, +Sg =D Production Constraints: P. - kn,W, -0, +U, = 0 specifically: P - knW, -0, +U, = 0 Pg kngW-0+Ug = 0 Finally, we need constraints defining: . Initial Workforce size: Wo . Starting Inventory: 1 . Final Desired Inventory: Ig And, of course, the general constraint forcing all variables to be > 0 Total Hiring Cost Total Firing Cost 8 8 8 Minimize 800, +1250 + 8.5, t=1 t=1 t=1 Total Holding Cost Employee Constraints: W -W. -H, +F = 0, W -W, -H2 +F2 = 0, W-W-Hz +F3 = 0, W4-W-H4 +F4 = 0, W-W. -H, +F, = 0, W. -W5 - H6 +F6 = 0, W-W. -H, +F, = 0, W -W. - He + Fg = 0; Inventory Constraints: + + P. -1, +1. = 420 P2 12 +11 = 280 P2 13 +12 = 460 P,-1+1] = 190 P - 13 + 14 = 310 P-16 +1; = 145 P,-1, +1, -110 P-12 +1, =125 Production Constraints: P, kn,W, -0, +U, = 0 specifically: P. - kn,W- 0, +U, = 0) Po knW 0+Ug = 0 Month #Work Days Forecast Demand net Min # Workers Cum. Prod. C.Units/Worker C. Net Demand End. Inv #Units/worker Prod. Jan 22.00 220.00 17.53 7.53 220.00 29.23 346 346 126 Feb 16.00 280.00 5.47 13.00 500.00 38.46 252 598 98 Mar 23.00 460.00 7.87 20.87 960.00 46.00 362 960 0 Apr 20.00 190.00 6.84 27.71 1150.00 41.50 315 1275 125 May 21.00 310.00 7.18 34.89 1460.00 41.84 330 1605 145 Jun 22.00 145.00 7.53 42.42 1605.00 37.84 346 1951 346 Jul 21.00 110.00 7.18 49.60 1715.00 34.57 330 2281 566 Aug 22.00 225.00 7.53 57.13 1940.00 33.96 346 2627 687 Knt: the number of units produced by one worker in period t 20 Production levels Constraints: P. 7.53W, = 0 P2-5,47W = 0 Pz 7.87W2 = 0 P4 -6.84W, = 0 P3 7.18W, = 0 P-7.53W = 0 P. 7.18W, = 0 P - 7.53W, = 0