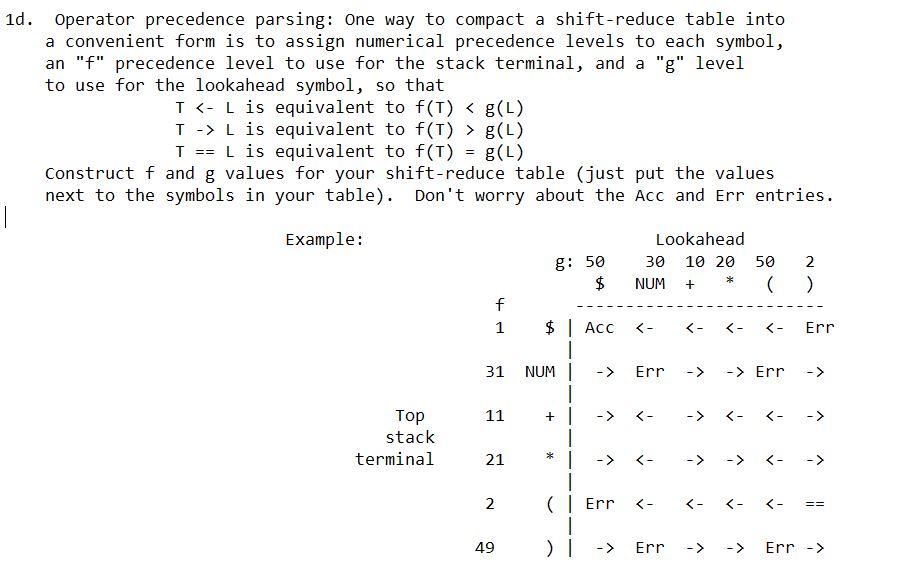
The expression grammar E ==> E + E E ==> E *E E ==> ( E) E ==> NUM Lookahead + ( $ NUM ) could have the shift-reduce table at right: Here, "ACC" means "Accept" for a success, and "Err" means an error, since this combination cannot legally occur. Err -> Top stack terminal + 1 -> -> Err -> * * ** * * $ E * * X 4 So for example the expression 3* ( 4 + 5 ) would have a parse Stack Remaining input Comment $ 3 ( 4 + 5 ) $ $ so reduce $ E (E + 5 ) $ ( ) so reduce $ E (E+ E + ) so reduce $ E (E ( ) so shift (E) $ ) -> $ so reduce $ E * E $ -> $ so reduce $ E $ ACC $ so accept, done. * * * * * ) E * * 1a. Do a shift-reduce parse of 2 * 3 + 1. Do a shift-reduce parse of 2 * 3 * 1. Is multiplication left or right associative (i.e. is the left multiplication reduced first or the right)? Do a shift-reduce parse of 2 * 3* ( 4 + 5* (6 + 7)). 1b. Construct a shift-reduce table for the expressions in Atto-c. The terminals involved are $ high precedence binary operators + - = == != && Il low precedence binary operator IDENT NUM ! - (unary minus) You can treat the symbols on one row as a group, so your table will only need 14 rows and columns. The binary operators are listed in precedence order, so * / should be done before + - which are before Lis equivalent to f(T) > g(L) T == L is equivalent to f(T) = g(L) Construct f and g values for your shift-reduce table (just put the values next to the symbols in your table). Don't worry about the Acc and Err entries. Example: 8: 50 Lookahead 30 10 20 NUM + 50 ( 2 ) $ f 1 -> Err -> 11 + 1 -> Top ack terminal 21 -> 1 1 2 Err Err -> Err-> The expression grammar E ==> E + E E ==> E *E E ==> ( E) E ==> NUM Lookahead + ( $ NUM ) could have the shift-reduce table at right: Here, "ACC" means "Accept" for a success, and "Err" means an error, since this combination cannot legally occur. Err -> Top stack terminal + 1 -> -> Err -> * * ** * * $ E * * X 4 So for example the expression 3* ( 4 + 5 ) would have a parse Stack Remaining input Comment $ 3 ( 4 + 5 ) $ $ so reduce $ E (E + 5 ) $ ( ) so reduce $ E (E+ E + ) so reduce $ E (E ( ) so shift (E) $ ) -> $ so reduce $ E * E $ -> $ so reduce $ E $ ACC $ so accept, done. * * * * * ) E * * 1a. Do a shift-reduce parse of 2 * 3 + 1. Do a shift-reduce parse of 2 * 3 * 1. Is multiplication left or right associative (i.e. is the left multiplication reduced first or the right)? Do a shift-reduce parse of 2 * 3* ( 4 + 5* (6 + 7)). 1b. Construct a shift-reduce table for the expressions in Atto-c. The terminals involved are $ high precedence binary operators + - = == != && Il low precedence binary operator IDENT NUM ! - (unary minus) You can treat the symbols on one row as a group, so your table will only need 14 rows and columns. The binary operators are listed in precedence order, so * / should be done before + - which are before Lis equivalent to f(T) > g(L) T == L is equivalent to f(T) = g(L) Construct f and g values for your shift-reduce table (just put the values next to the symbols in your table). Don't worry about the Acc and Err entries. Example: 8: 50 Lookahead 30 10 20 NUM + 50 ( 2 ) $ f 1 -> Err -> 11 + 1 -> Top ack terminal 21 -> 1 1 2 Err Err -> Err->