The external path length of a full binary tree is the sum, taken over all nil leaves of the tree, of the depth of each leaf. Given the following binary search tree, in which internal nodes are shown as circles and external nodes (leaves; nil pointers) are shown as small boxes: 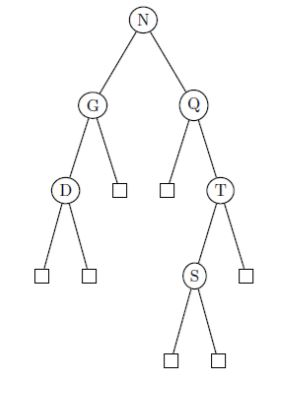a) Calculate the external path length. b) Is there a binary search tree on the same set of letters, {D, G, N, Q, S, T}, that has lower external path length? Either give such a tree and how it is formed from the original BST or prove it does not exist. c) Can the nodes in the original BST be colored red and black so as to form a proper red-black tree? If so, show how to color them; if not, prove it.