Question: The first term of an arithmetic sequence is 27. The common difference of the sequence is 6. What is the sum of the first 30

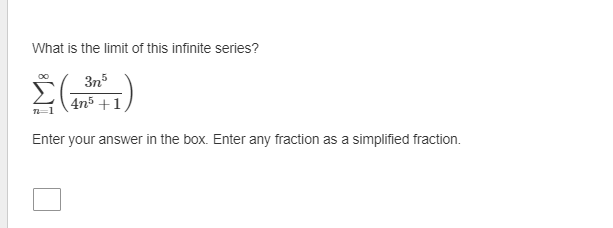


![box. Enter any fraction as a simplified fraction. [ ] What is](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6708f8041fd5c_0286708f8040e77c.jpg)
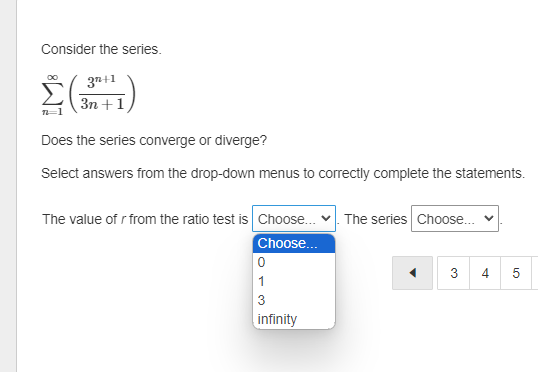
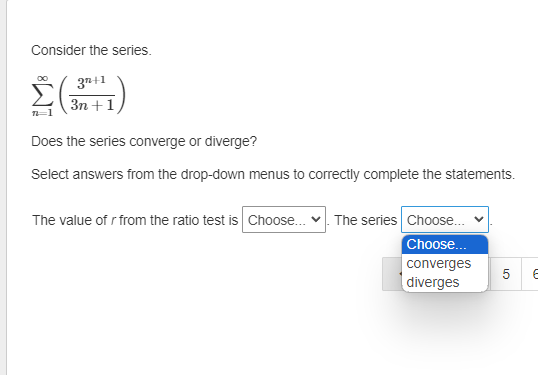
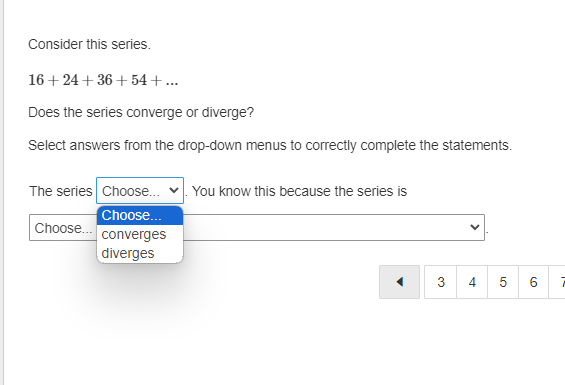
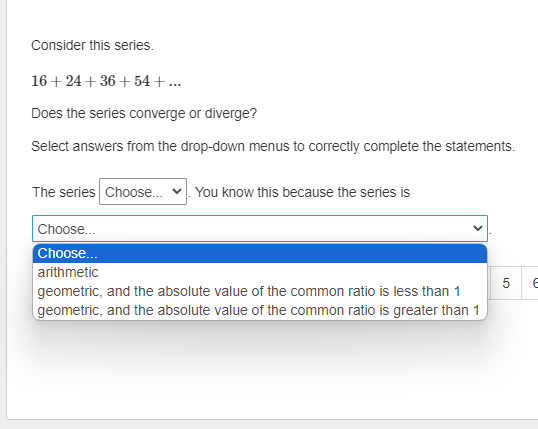
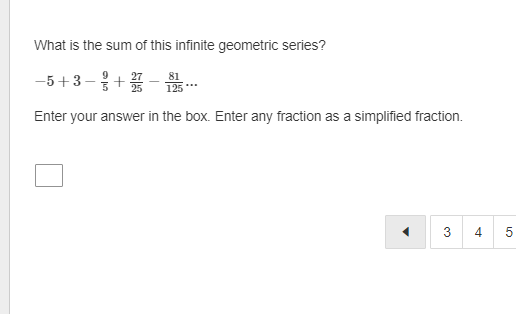

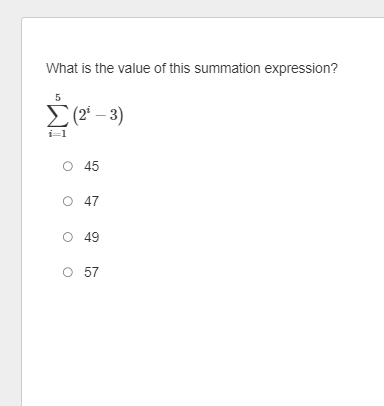
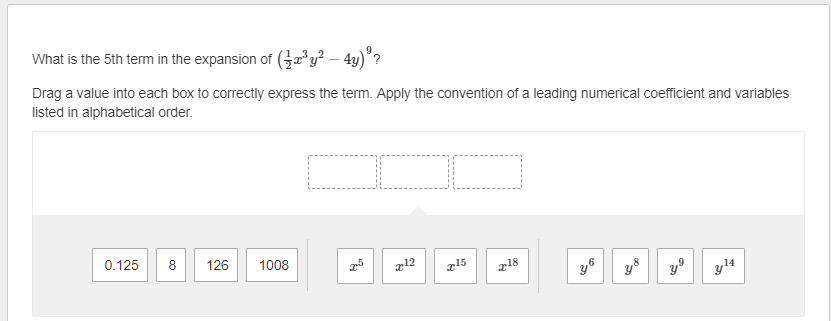
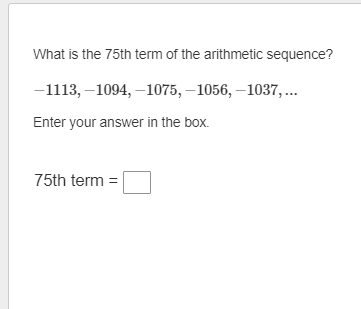
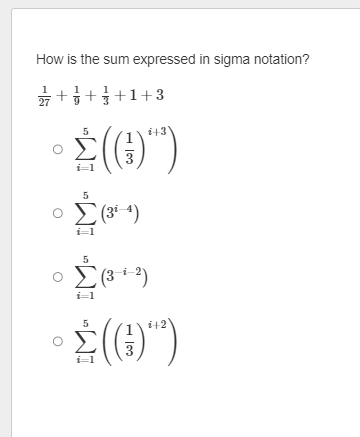
The first term of an arithmetic sequence is 27. The common difference of the sequence is 6. What is the sum of the first 30 terms of the sequence? Enter your answer in the box. sUm :D \f9 What is the 5th term in the expansion of (zz*y 4y) ? Drag a value into each box to correctly express the term. Apply the convention of a leading numerical coefficient and variables listed in alphabetical order. What is the limit of this infinite series? = In Z (4n5 +1 ) n=1 Enter your answer in the box. Enter any fraction as a simplified fraction. [ ] What is the 75th term of the arithmetic sequence? 1113, 1094, 1075, 1056, 1037, ... Enter your answer in the box. 75th term = D How is the sum expressed in sigma notation? 27 + + +1+3 143 O 09 # I'M 5 O S (31 4) 5 o (3 2) 5 142 OThe first term of a geometric sequence is 2100. The common ratio of the sequence is 0.1. What is the 7th term of the sequence? Enter your answer in the box. 7th term = E The nth term of a sequence is represented by in\":lg . What iz the limit of the the nth term as n becomes increasingly large? _\\ A L The limit of the nth term does not exist. Consider the series. > (3r1) n=1 Does the series converge or diverge? Select answers from the drop-down menus to comectly complete the statements. The value of r from the ratio test is . The series . Consider the series. i ( 3l 1 ) o Int1 Does the series converge or diverge? Select answers from the drop-down menus to comectly complete the statements. The value of r from the ratio test is _ The series _ |0 1 3 infinity ] Consider the series. gn +1 S 3n + 1 Does the series converge or diverge? Select answers from the drop-down menus to correctly complete the statements. The value of r from the ratio test is Choose... v The series Choose... Choose... converges 5 divergesConsider this series. 16 + 24 + 36 + 54 + ... Does the series converge or diverge? Select answers from the drop-down menus to correctly complete the statements. The series Choose... You know this because the series is Choose... Choose.. converges diverges 3 4 5 6Consider this series. 16+ 24+ 36+ 54 + ... Does the series converge or diverge? Select answers from the drop-down menus to correctly complete the statements. The series . You know this because the series is e ] arithmetic | geometric, and the absolute value of the common ratio is less than 1 geometric, and the absolute value of the common ratio is greater than 1 | D | E What is the sum of this infinite geometric series? 9 a7 E1 Enter your answer in the box. Enter any fraction as a simplified fraction. L] The first term of a geometric sequence is 15, and the 5th term of the sequence is %. What are the geometric means between these terms? Enter your answer by filling in the boxes to comectly complete the geometric sequence. Enter any fractions as simplified fractions. G
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


