The following problem uses the Lisp coding language.
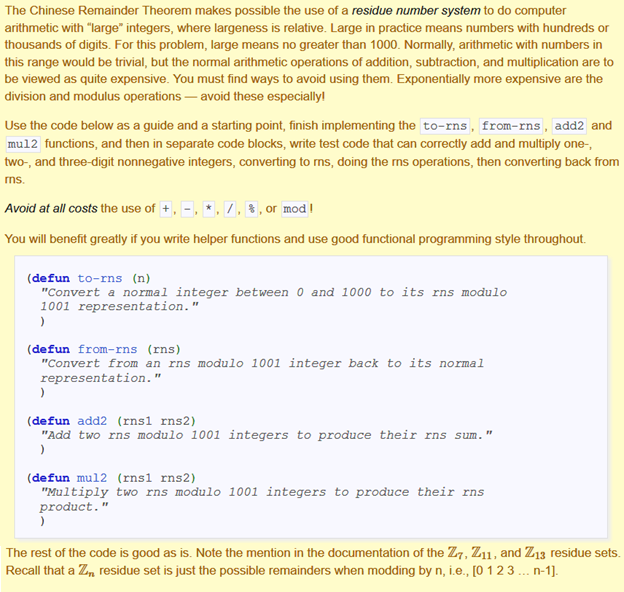
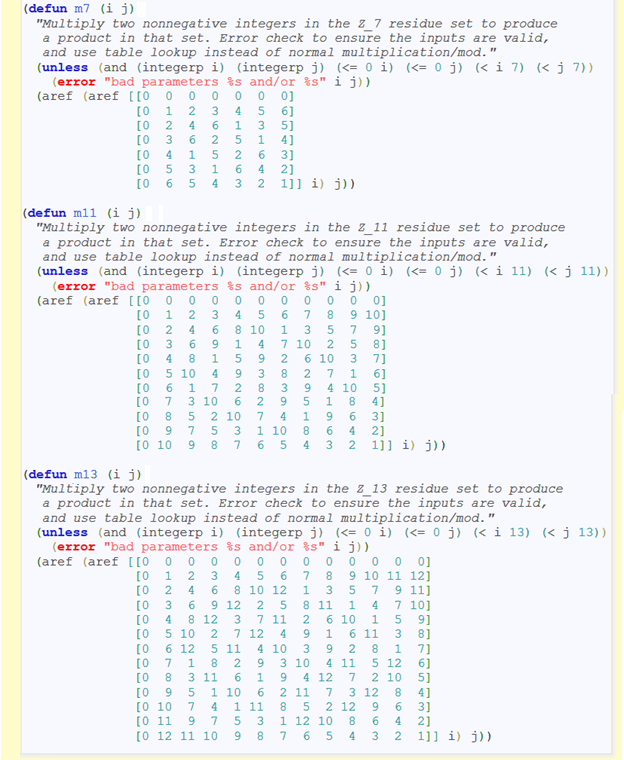
The Chinese Remainder Theorem makes possible the use of a residue number system to do computer arithmetic with "large" integers, where largeness is relative. Large in practice means numbers with hundreds or thousands of digits. For this problem, large means no greater than 1000. Normally, arithmetic with numbers in this range would be trivial, but the normal arithmetic operations of addition, subtraction, and multiplication are to be viewed as quite expensive. You must find ways to avoid using them. Exponentially more expensive are the division and modulus operations-avoid these especially Use the code below as a guide and a starting point, finish implementing the to-rns, from-rns, add2 and mu12 functions, and then in separate code blocks, write test code that can correctly add and multiply one- two-, and three-digit nonnegative integers, converting to ns, doing the ms operations, then converting back fromm ms. Avoid at all costs the use of +, -, *, /, % , or mod! You will benefit greatly if you write helper functions and use good functional programming style throughout. (defun to-rns (n) "Convert a normal integer between 0 and 1000 to its rns modulo 1001 representation." (defun from-rns (rns) "Convert from an rns modulo 1001 integer back to its normal representation. (defun add2 (rnsl rns2) "Add two rns modulo 1001 integers to produce their rns sum." (defun mul2 (rnsl rns2) "Multiply two rns modulo 1001 integers to produce their rns product." The rest of the code is good as is. Note the mention in the documentation of the Z, Z11, and Z13 residue sets Recall that a Zn residue set is just the possible remainders when modding by n, i.e, [0 123 n-1] The Chinese Remainder Theorem makes possible the use of a residue number system to do computer arithmetic with "large" integers, where largeness is relative. Large in practice means numbers with hundreds or thousands of digits. For this problem, large means no greater than 1000. Normally, arithmetic with numbers in this range would be trivial, but the normal arithmetic operations of addition, subtraction, and multiplication are to be viewed as quite expensive. You must find ways to avoid using them. Exponentially more expensive are the division and modulus operations-avoid these especially Use the code below as a guide and a starting point, finish implementing the to-rns, from-rns, add2 and mu12 functions, and then in separate code blocks, write test code that can correctly add and multiply one- two-, and three-digit nonnegative integers, converting to ns, doing the ms operations, then converting back fromm ms. Avoid at all costs the use of +, -, *, /, % , or mod! You will benefit greatly if you write helper functions and use good functional programming style throughout. (defun to-rns (n) "Convert a normal integer between 0 and 1000 to its rns modulo 1001 representation." (defun from-rns (rns) "Convert from an rns modulo 1001 integer back to its normal representation. (defun add2 (rnsl rns2) "Add two rns modulo 1001 integers to produce their rns sum." (defun mul2 (rnsl rns2) "Multiply two rns modulo 1001 integers to produce their rns product." The rest of the code is good as is. Note the mention in the documentation of the Z, Z11, and Z13 residue sets Recall that a Zn residue set is just the possible remainders when modding by n, i.e, [0 123 n-1]
