the following question

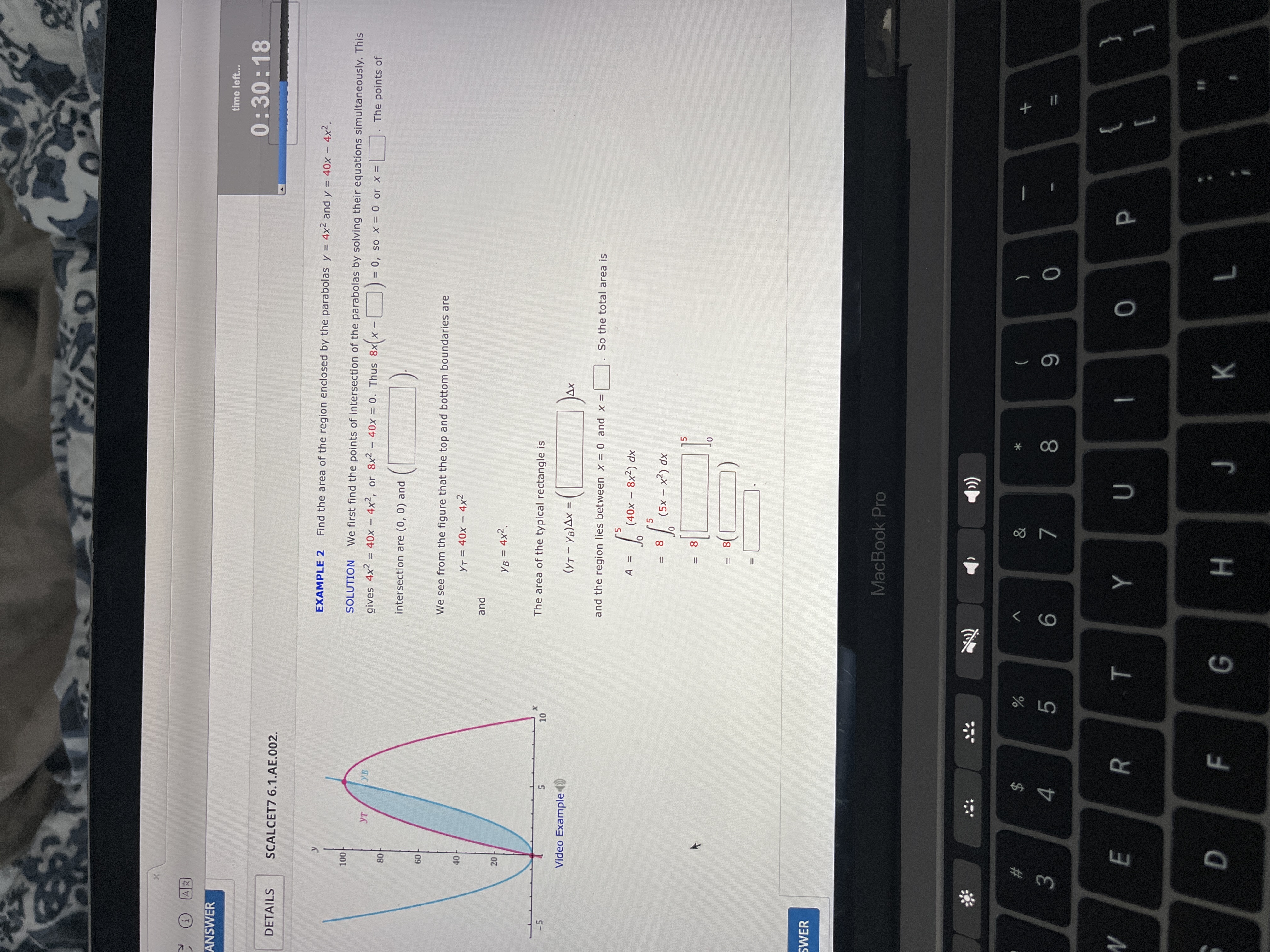i AZ ANSWER time left.. 0: 30: 18 DETAILS SCALCET7 6.1.AE.002. EXAMPLE 2 Find the area of the region enclosed by the parabolas y = 4x2 and y = 40x - 4x2. 100 SOLUTION We first find the points of intersection of the parabolas by solving their equations simultaneously. This yB gives 4x2 = 40x - 4x2, or 8x2 - 40x = 0. Thus 8x(x - = 0, so x = 0 or x =. The points of 80 intersection are (0, 0) and 60 We see from the figure that the top and bottom boundaries are 40 YT = 40x - 4x2 and 20 YB = 4x2. 10 The area of the typical rectangle is Video Example () (YT - YB)AX = and the region lies between x = 0 and x = . So the total area is 10 ( 40 x - 8 x 2 ) dx = 8 / ( 5x - * 2 ) dx - 8 SWER MacBook Pro $ % 5 6 7 8 9 O E R T Y U O P D F G H C K