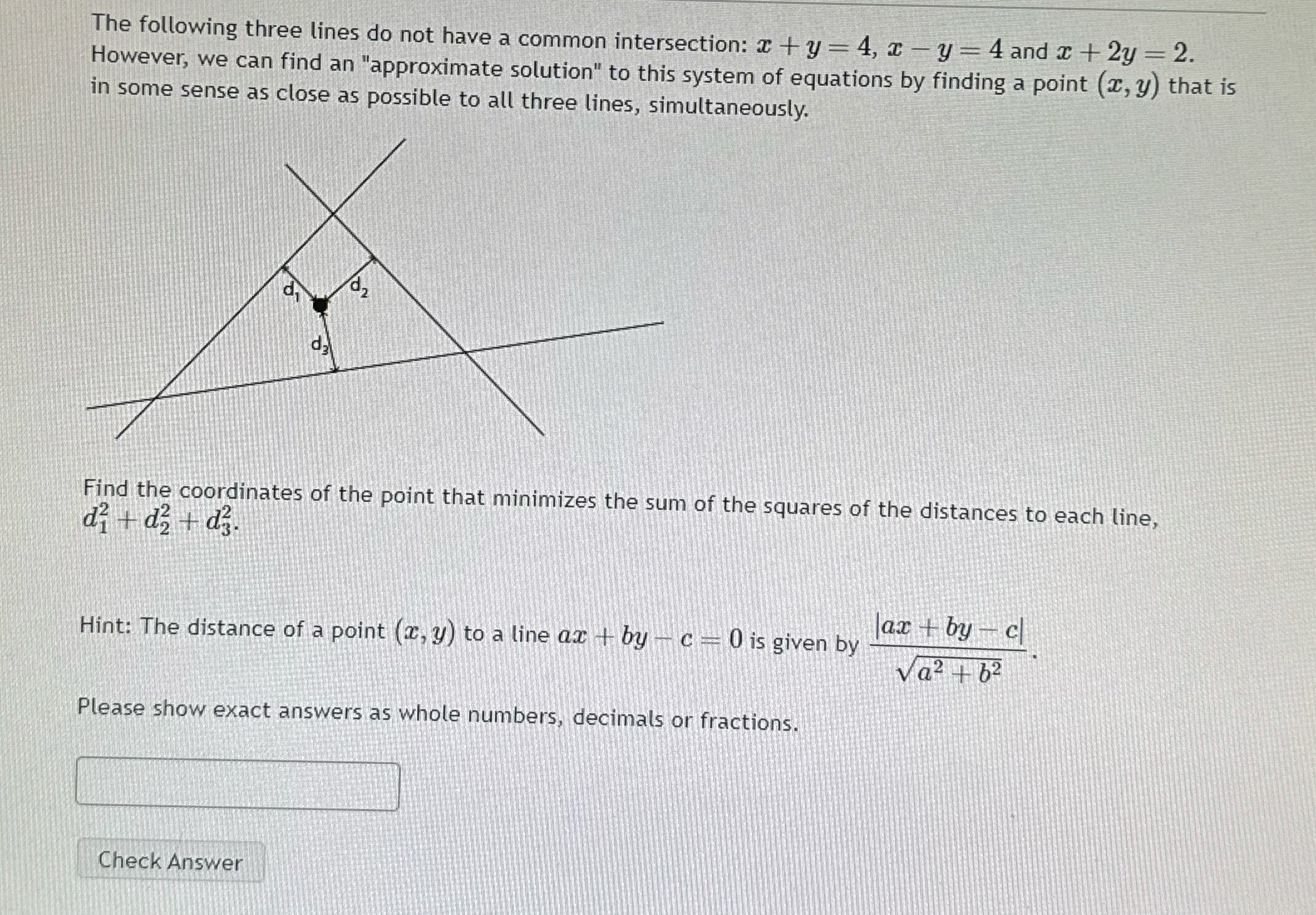
The following three lines do not have a common intersection: x+y=4, x-y=4 and x + 2y = 2. However, we can find an "approximate solution" to this system of equations by finding a point (x, y) that is in some sense as close as possible to all three lines, simultaneously. 182 Find the coordinates of the point that minimizes the sum of the squares of the distances to each line, d + d + d. Hint: The distance of a point (x, y) to a line ax + by c=0 is given by Please show exact answers as whole numbers, decimals or fractions. Check Answer ax+by c Va+b