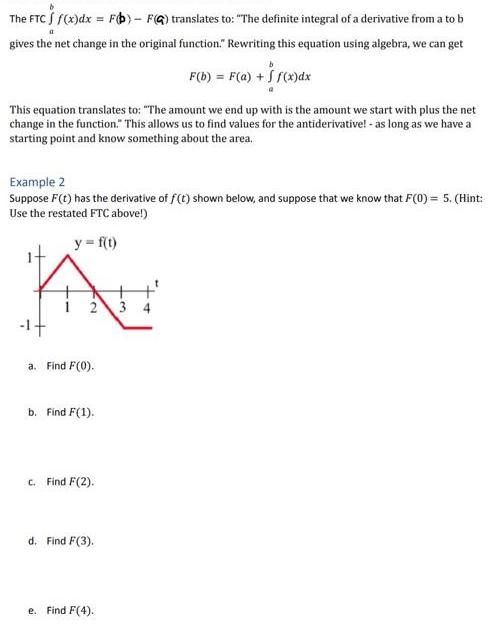
The FTC / f(x)dx = F(b)- F(G) translates to: "The definite integral of a derivative from a to b gives the net change in the original function." Rewriting this equation using algebra, we can get This equation translates to: "The amount we end up with is the amount we start with plus the net change in the function. This allows us to find values for the antiderivative! - as long as we have a starting point and know something about the area. Example 2 Suppose F(t) has the derivative of f(t) shown below, and suppose that we know that F(0) = 5. (Hint: Use the restated FTC above!) y = f(t) ++ 2 3 4 a. Find F(0). b. Find F(1). c. Find F(2). F(b) = F(a) + f f(x)dx + f(x)dx d. Find F(3). e. Find F(4).