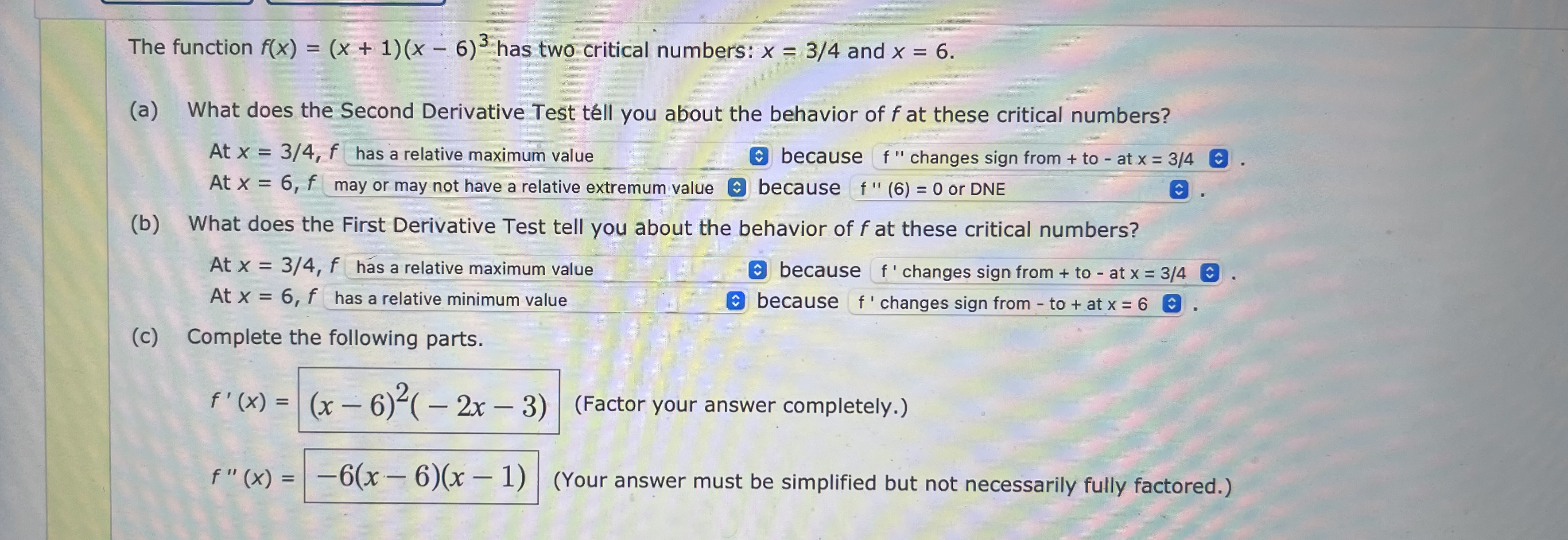
The function $f(x)=(x+1)(x-6{)}^3$ has two critical numbers: $x=\frac{3}{4}$ and $x=6.$

$($a$)$ What does the Second Derivative Test tell you about the behavior of $f$ at these critical numbers?

At $x=\frac{3}{4},f$ has a relative maximum value

because

$f"$ changes sign from $+$ to $-$ at $x=\frac{3}{4}$

At $x=6,f$

may or may not have a relative extremum value $$ because $f^{\text{'}\text{'}}(6)=0$ or DNE

$($b$)$ What does the First Derivative Test tell you about the behavior of $f$ at these critical numbers?

At $x=\frac{3}{4},f$ has a relative maximum value

e because $f^{\text{'}}$ changes sign from $+$ to $-$ at $x=\frac{3}{4}$

$$

At $x=6,f$ has a relative minimum value

$(2)$ because $f^{\text{'}}$ changes sign from $-$ to $+$ at $x=6$

$($c$)$ Complete the following parts.

$f^{\text{'}}(x)=($Factor your answer completely.$)$

$f^{\text{'}\text{'}}(x)=($Your answer must be simplified but not necessarily fully factored.$)$