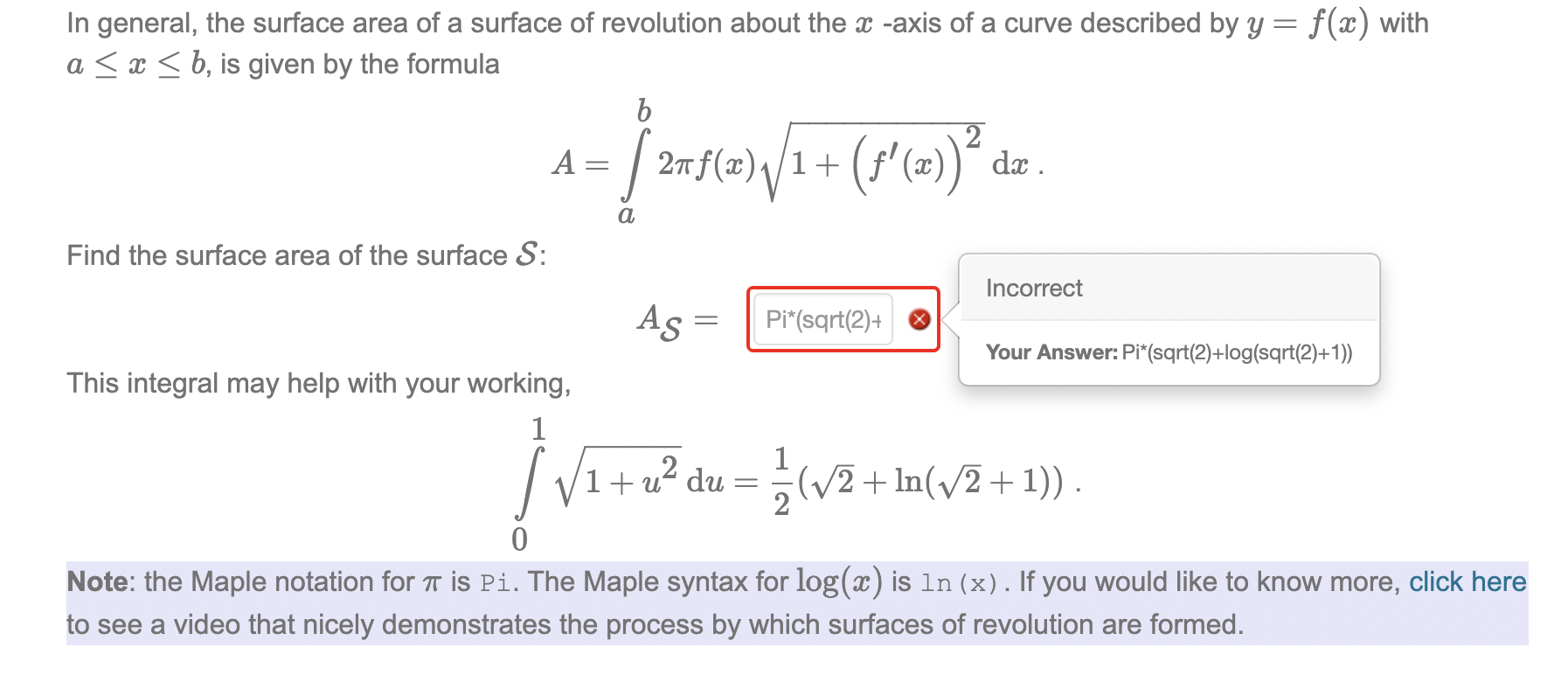
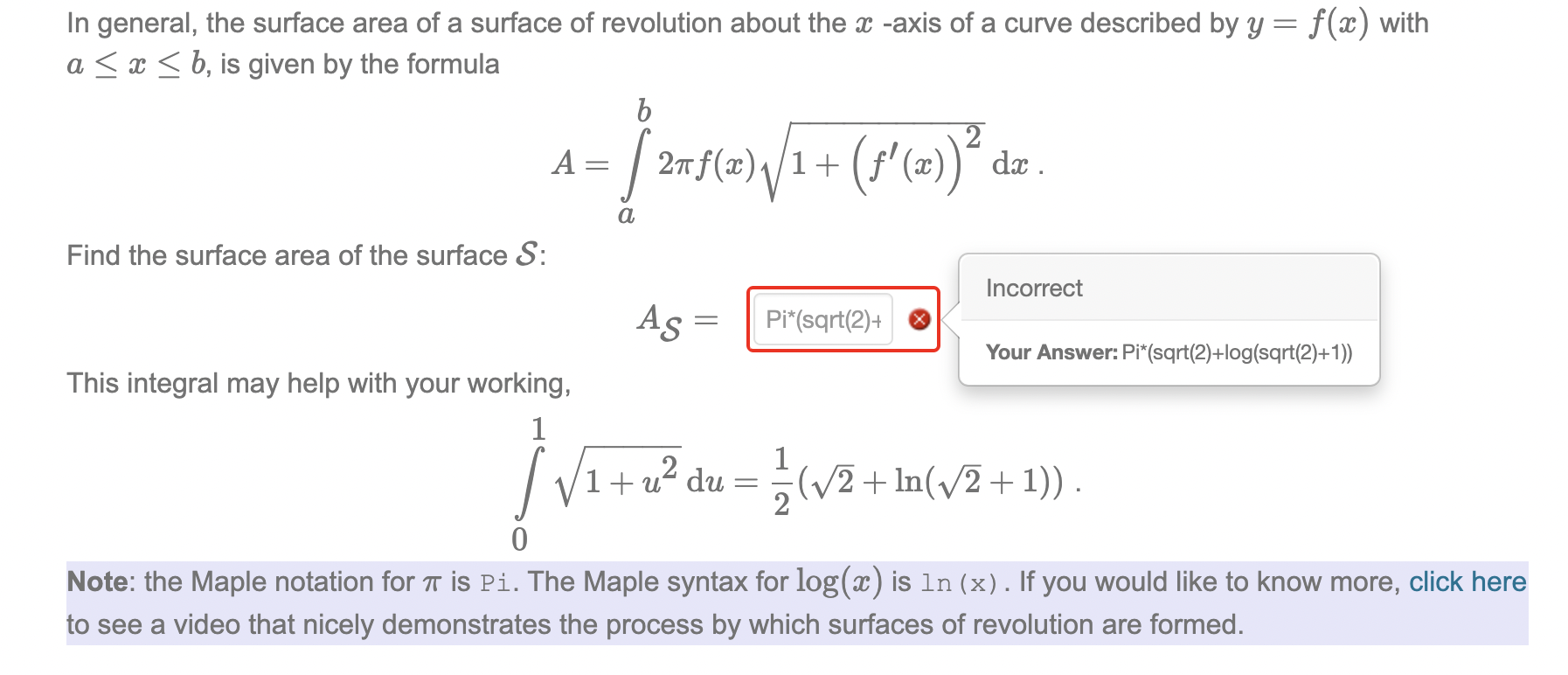
The function f(w) : 61: for m : 0 to 00 can be rotated about the z axis to form a surface of revolution 8, which looks like a traffic cone (if you chop off the infinite taill). Surface of revolution 8 Traffic Cones The Duke of Wellington, by Patrick Morgan CC-BY 2.0 In general, the surface area of a surface of revolution about the a: -axis of a curve described by y = ax) with a S a: S b, is given by the formula I) A=f21rf(a:) 1+ (fl($))2 dw. Find the surface area of the surface 8: J Incorrect A 5 = Pi*(sqrt(2)+ o \\ 1 Your Answer: Pi*(sqrt(2)+log(sqrt(2)+1)) This integral may help with your working, \\ 1 fl/lFuzduz/i-l-ln/i-l-l. 0 Note: the Maple notation for 71' is Pi. The Maple syntax for 10g(m) is ln (x) . If you would like to know more, click here to see a video that nicely demonstrates the process by which surfaces of revolution are formed