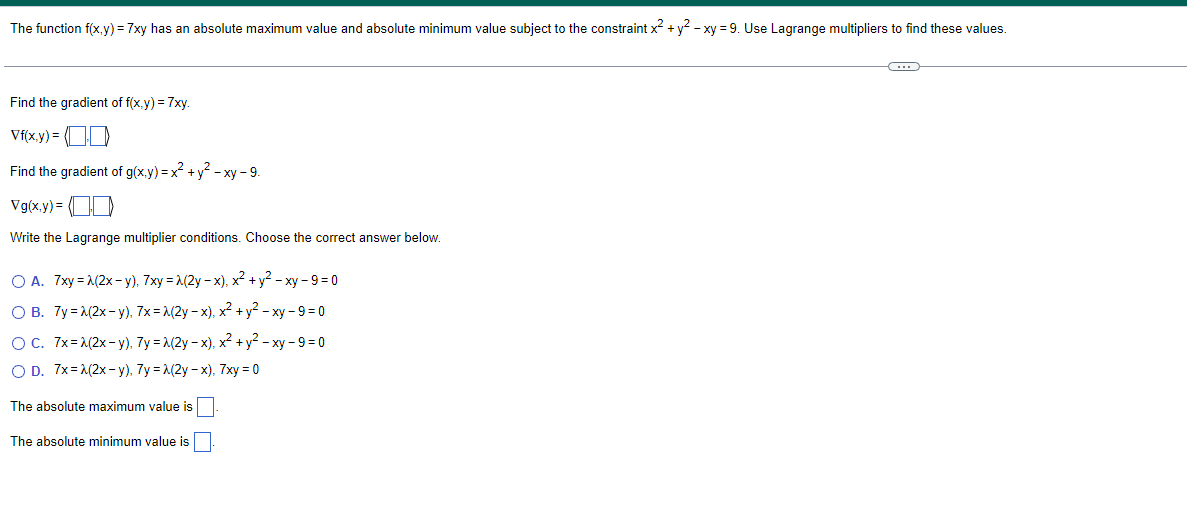
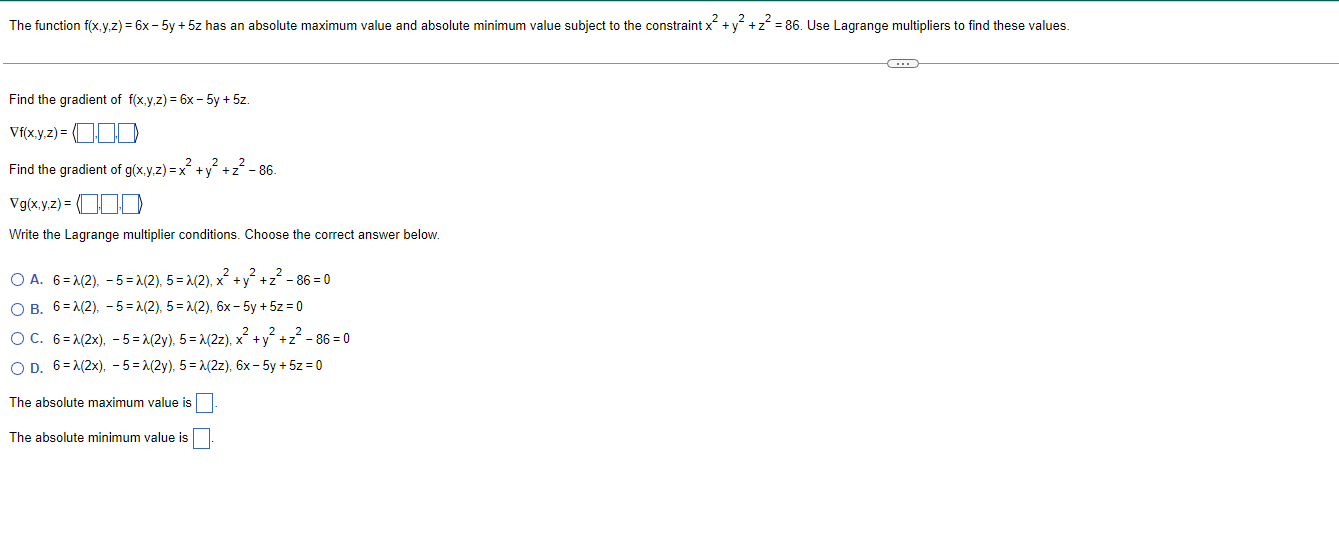
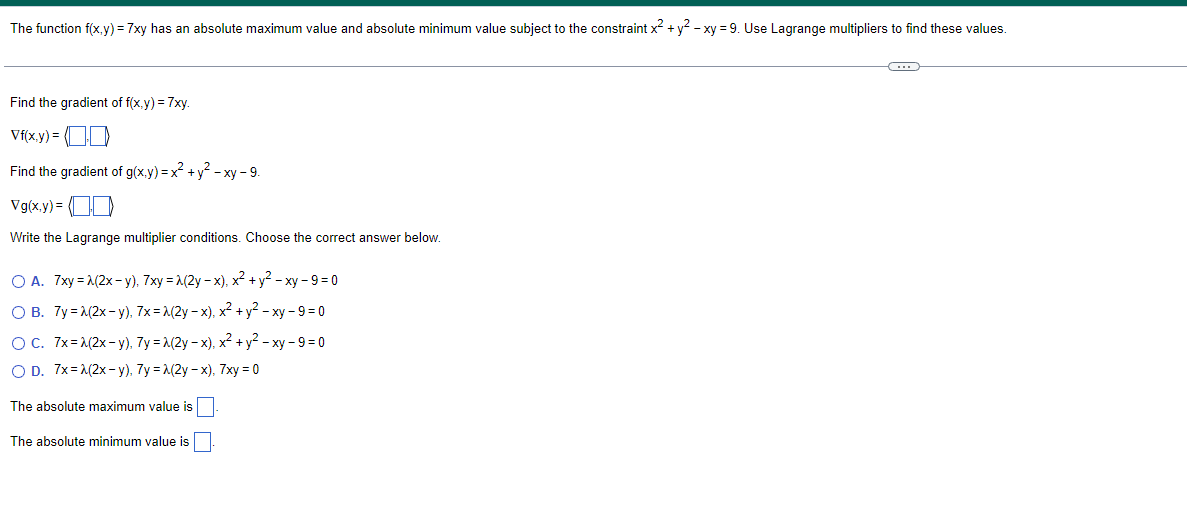
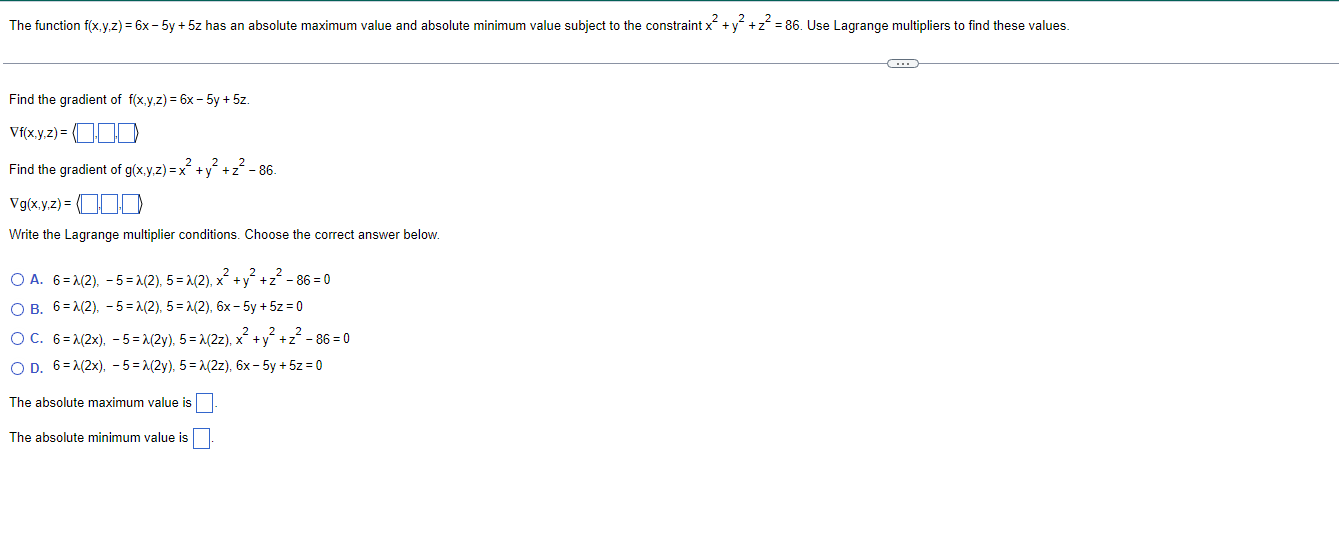
The function f(x,y) = 7xy has an absolute maximum value and absolute minimum value subject to the constraint x" + y- - xy =9. Use Lagrange multipliers to find these values. Find the gradient of f(x,y) = 7xy. Vf(x.y) = (0 Find the gradient of g(x,y) = x~+ y - xy - 9. Vg(x.y) = Write the Lagrange multiplier conditions. Choose the correct answer below. O A. 7xy =1(2x - y). 7xy = >(2y -x). x2+ y2 - xy- 9=0 O B. 7y=2(2x - y), 7x =>(2y -x), x2 + y2 - xy - 9=0 O C. 7x= 1(2x - y), 7y => (2y -x), x2 + y2 - xy- 9=0 O D. 7x=>(2x - y), 7y = >(2y -x). 7xy = 0 The absolute maximum value is The absolute minimum value isThe function f(x,y.z) = 6x - 5y + 5z has an absolute maximum value and absolute minimum value subject to the constraint x"+y+ 2" =86. Use Lagrange multipliers to find these values. Find the gradient of f(x,y,z) = 6x - 5y + 5z. Vf(x. y.z) = (0.0) Find the gradient of g(x,y,z) =x-+y~+z--86. Vg(x.y.z) = (0.0) Write the Lagrange multiplier conditions. Choose the correct answer below. O A. 6=1(2), - 5=1(2), 5=1(2). x +y~+2-86=0 O B. 6=1(2), -5=>(2), 5=1(2), 6x - 5y + 52 = 0 O C. 6=1(2x), - 5=>(2y). 5=>(2z), x +y +2-86=0 O D. 6= A(2x), - 5=1(2y), 5=>(2z), 6x - 5y + 5z = 0 The absolute maximum value is The absolute minimum value is