Question: The general solution to d x d t = y d y d t = - 2 x - 2 y is x ( t
The general solution to
is
Which parts of the general solution accounts for the fact that the differential equations predict that the mass will oscillate about the zero position? Which parts of the general solution accounts for the fact that the amplitude of the oscillations decreases over time?
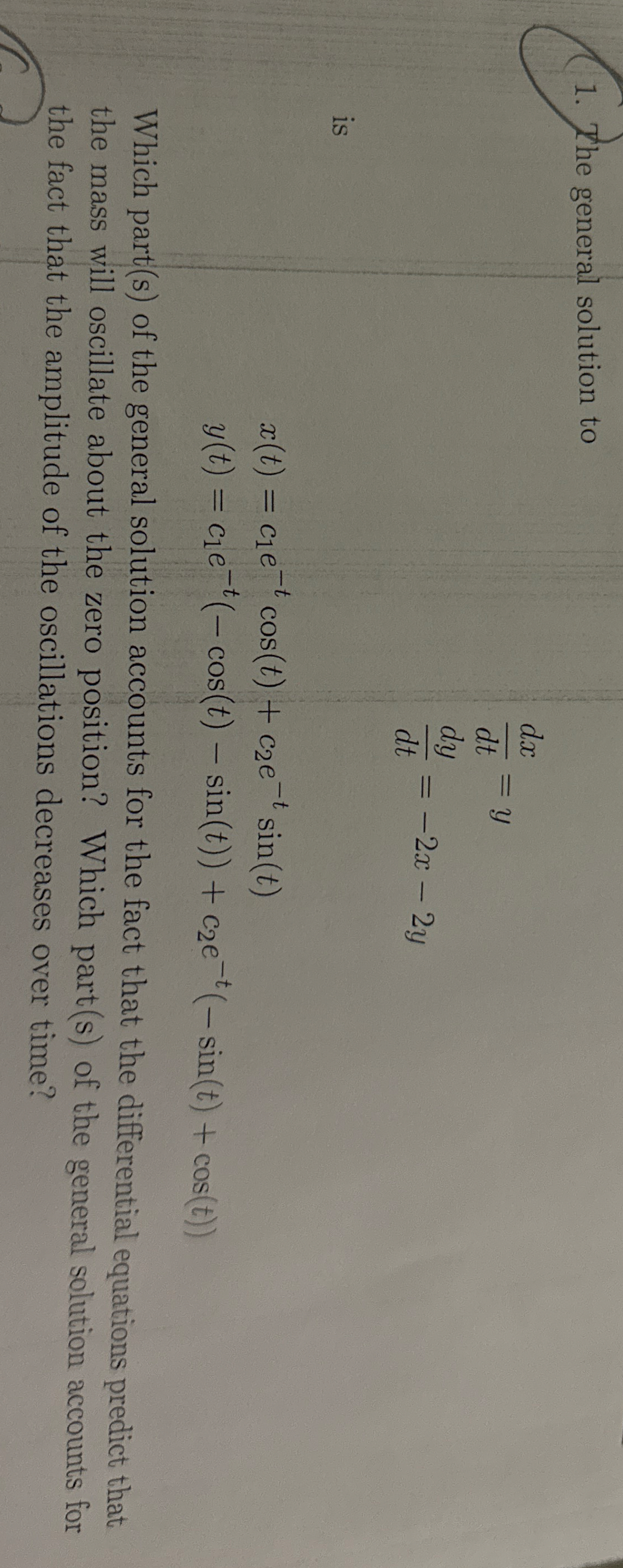
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


