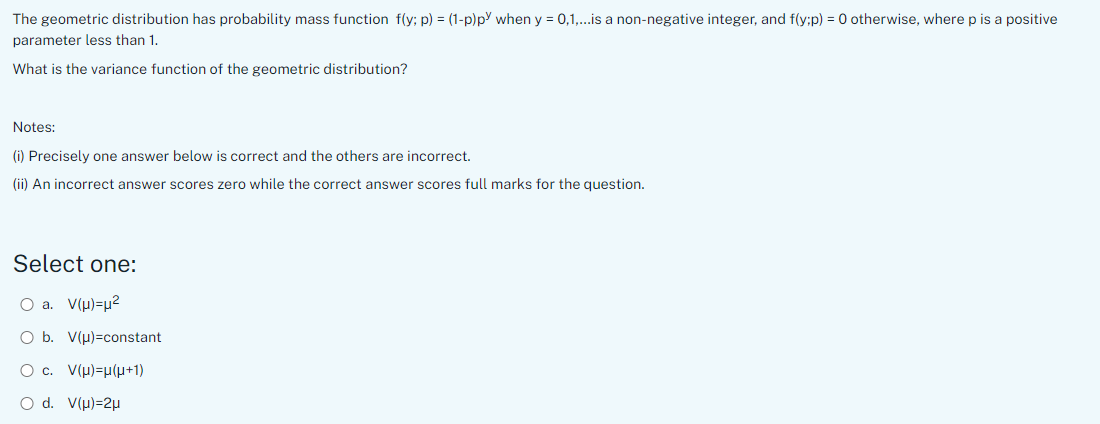
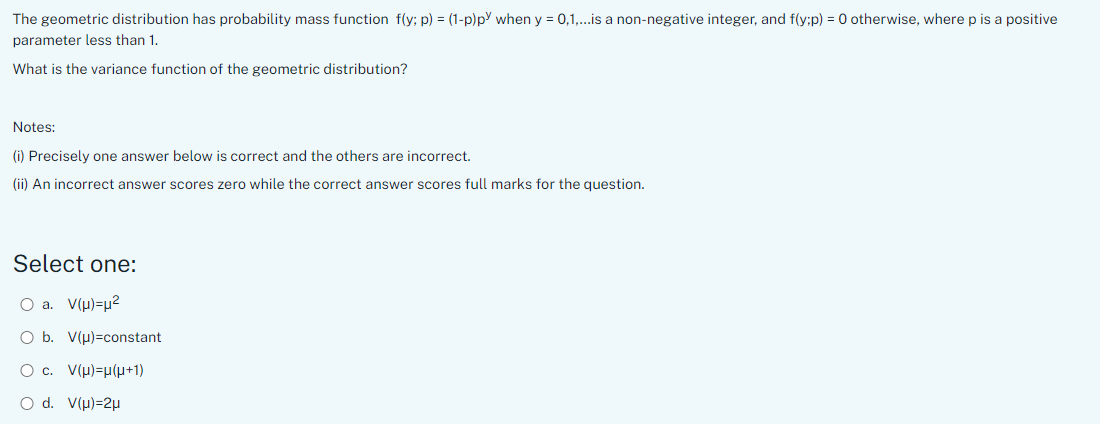
The geometric distribution has probability mass function f(y; p) = (1-p)p) when y = 0,1,...is a non-negative integer, and f(y;p) = 0 otherwise, where p is a positive parameter less than 1. What is the variance function of the geometric distribution? Notes: (i) Precisely one answer below is correct and the others are incorrect. (ii) An incorrect answer scores zero while the correct answer scores full marks for the question. Select one: O a. V(p)=12 O b. V(p)=constant O c. V(H)=H(H+1) O d. V(p)=2p