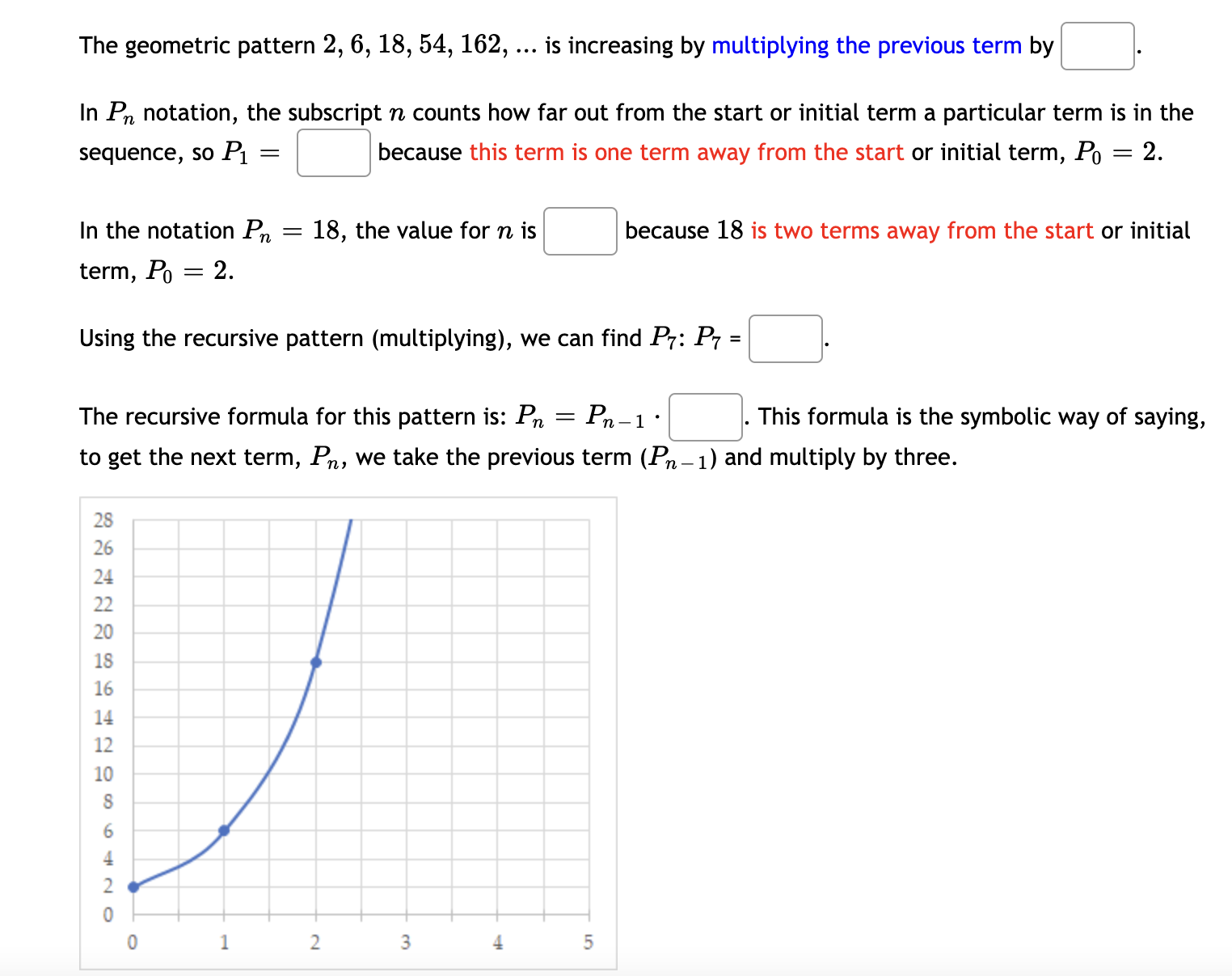
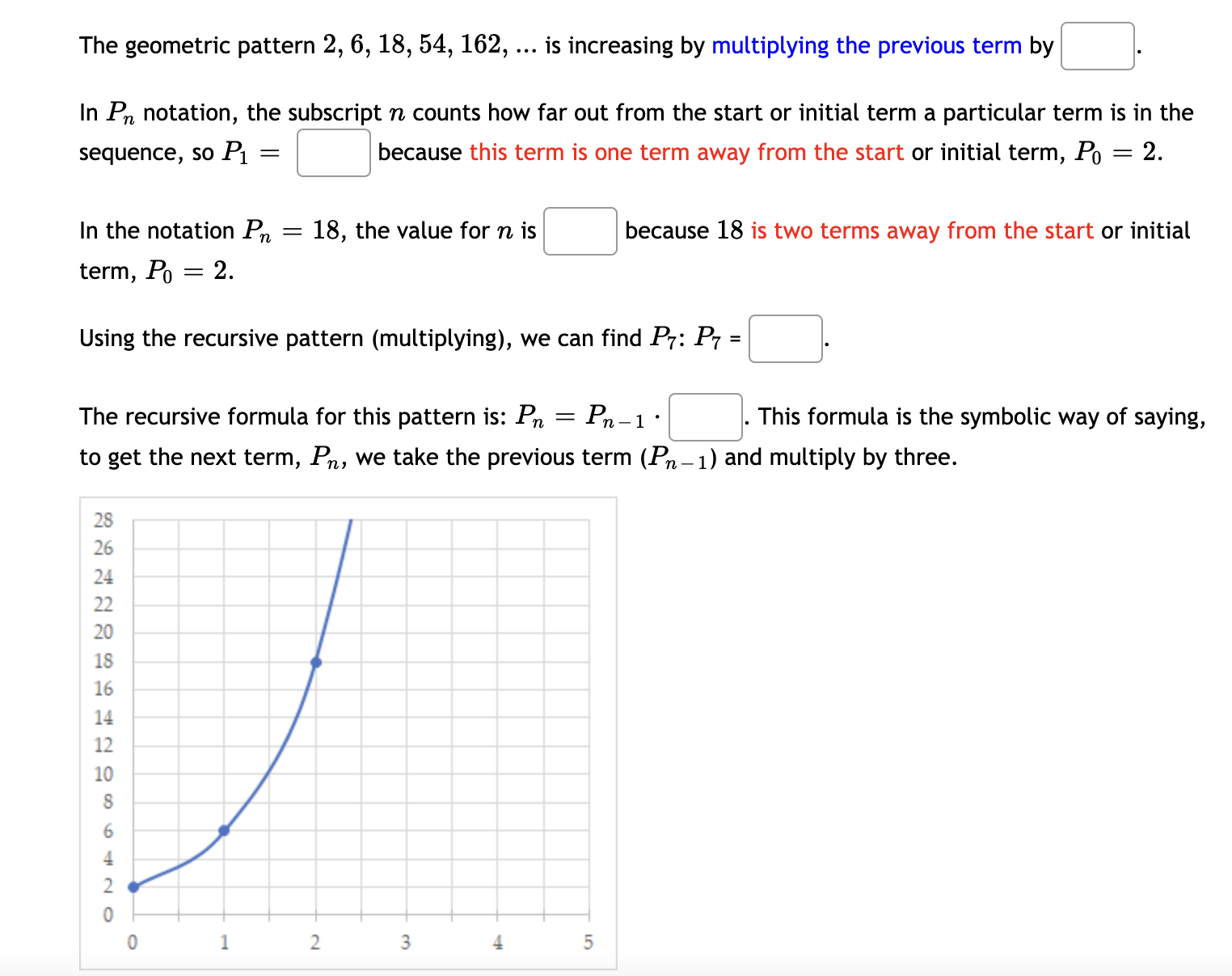
The geometric pattern 2, 6, 18, 54, 162, is increasing by multiplying the previous term by In P\" notation, the subscript n counts how far out from the start or initial term a particular term is in the sequence, 50 P1 2 because this term is one term away from the start or initial term, P0 = 2. In the notation Pn = 18, the value for n is because 18 is two terms away from the start or initial term, P0 = 2. Using the recursive pattern (multiplying), we can find P7: P7 = The recursive formula for this pattern is: P\" = T,_ 1 - . This formula is the symbolic way of saying, to get the next term, Pn, we take the previous term (Pn_1) and multiply by three. 'JI . The graph of this pattern shows |Select an answer v growth . This graph occurs because the ratio (multiplier) b between the terms is constant. . If R is the percent of increase or decrease then the ratio is b = 100 % + R % , decimal form, R% r = then the ratio is b = 1 + r. 100 . For b > 1, the sequence shows Select an answer v . For 0