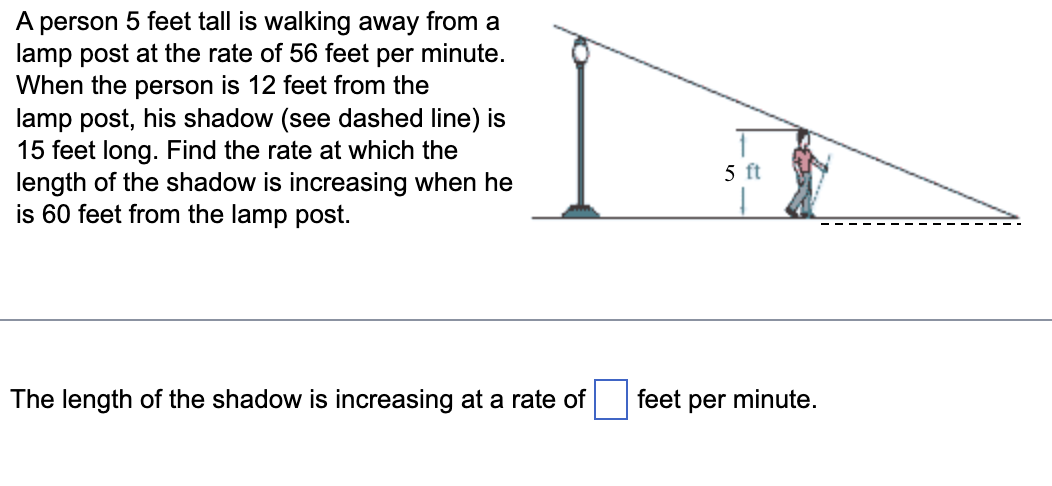
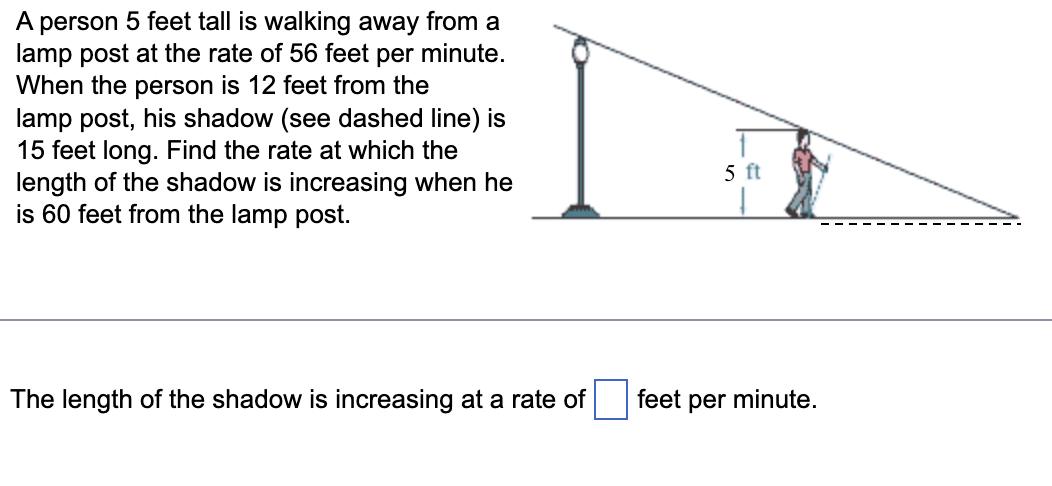
The graph 1::an2 + y2 = 100 is a circle having center at the origin and radius 10. a. Write the equation of the tangent lines at the points where x = 8. b. Graph the circle and the tangent lines. a. The line that is tangent to the circle at X: 8 and y = 6 is y = D. Researchers have found a correlation between respiratory rate and body mass in the first three years of life. This correlation can be expressed by the function log R(w) = 1.83 - 0.43 log (w), where w is the body weight (in kilograms) and R(w) is the respiratory rate (in breaths per minute). a. Find R'(w) using implicit differentiation. b. Find R'(w) by first solving the equation for R(w). c. Discuss the two procedures. Is there a situation when you would want to use one method over another? E) a. R'(w) = (Simplify your answer. Use integers or decimals for any numbers in the expression. Round to four decimal places as needed.) Suppose the average daily metabolic rate for certain types of animals can be expressed as a function of mass by r= 155.4m , where m is the mass of the animal (in kilograms) and r is the metabolic rate (in kcal per day). dm a. If the mass of an animal is changing at a rate of -, find dr at dr b. Determine - for a 140-kg animal that is gaining mass at a rate of 2 kg per day. a. If the mass of an animal is changing at a rate of am ar dt -, find dt arA rock is thrown into a still pond. The circular ripples move outward from the point of impact of the rock so that the radius of the circle formed by a ripple increases at the rate of 4 feet per minute. Find the rate at which the area is changing at the instant the radius is 6 feet. When the radius is 6 feet, the area is changing at approximately square feet per minute. (Round to the nearest thousandth as needed.) A person 5 feet tail is walking away from a lamp post at the rate of 56 feet per minute. When the person is 12 feet from the lamp post, his shadow (see dashed line) is 15 feet long. Find the rate at which the length of the shadow is increasing when he is 60 feet from the lamp post. The length of the shadow is increasing at a rate of D feet per minute