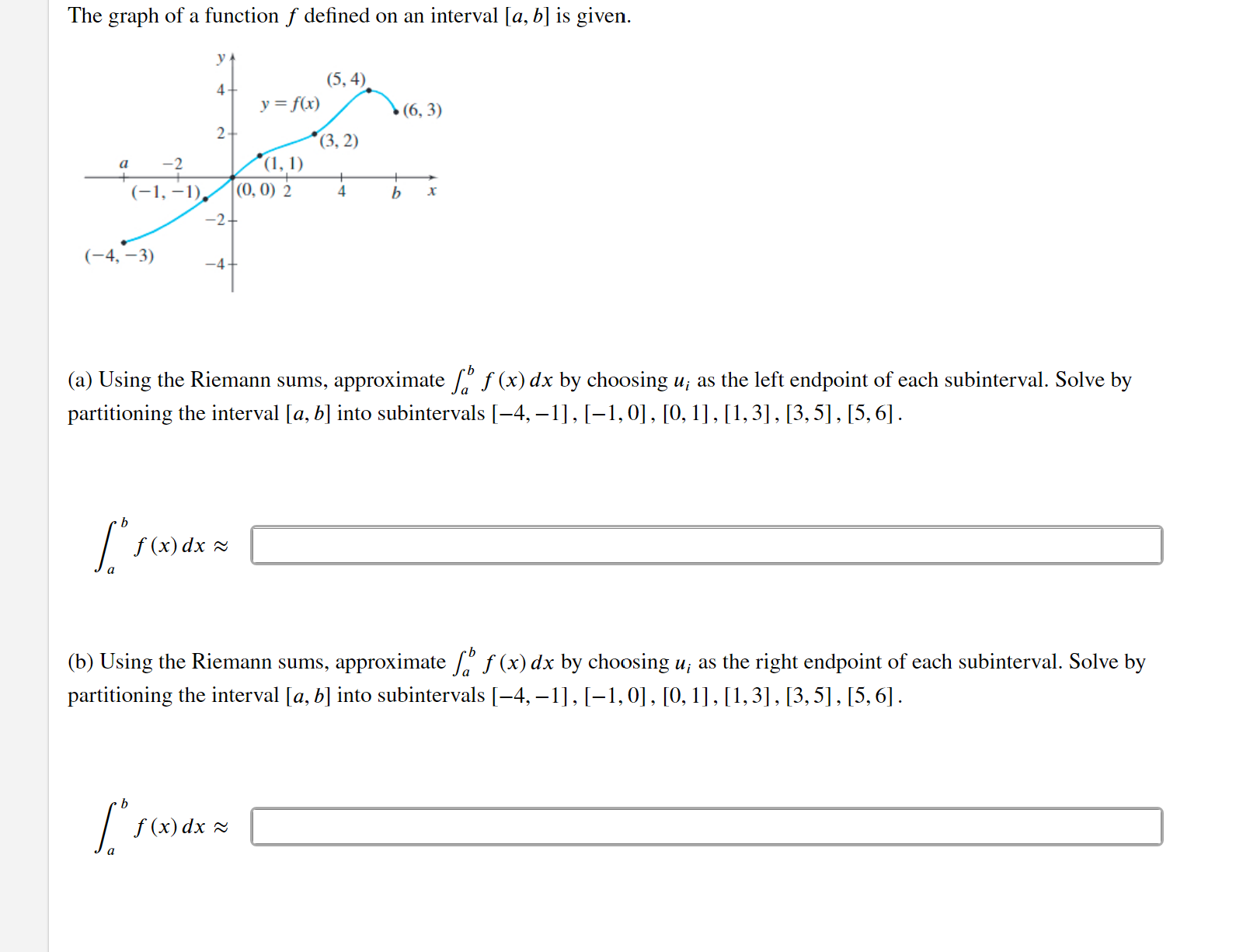
Question: The graph of a function f defined on an interval [a, b] is given. (5, 4) y = f(x) (6, 3) 2 (3, 2) a
![b] is given. (5, 4) y = f(x) (6, 3) 2 (3,](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6664f33019fda_8876664f32fe15ae.jpg)
The graph of a function f defined on an interval [a, b] is given. (5, 4) y = f(x) (6, 3) 2 (3, 2) a -2 (1, 1) (-1, -1). (0, 0) 2 b -2 (-4, -3) (a) Using the Riemann sums, approximate Sa f (x) dx by choosing u; as the left endpoint of each subinterval. Solve by partitioning the interval [a, b] into subintervals [-4, -1], [-1, 0], [0, 1], [1, 3], [3, 5], [5, 6]. / f ( x)dx ~ (b) Using the Riemann sums, approximate fa f (x) dx by choosing u; as the right endpoint of each subinterval. Solve by partitioning the interval [a, b] into subintervals [-4, -1], [-1, 0], [0, 1], [1, 3], [3, 5], [5, 6]. [ s ( )dx =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


