The Hamming distance between two strings x, y {0, 1}* is the number of places in which x and y differ. (If x and y do not have the same length, then the Hamming distance is infinite.) We use H(x, y) to denote the Hamming distance between x and y. For example, H(010, 010) = 0, H(011, 010) = 1, and H(0110, 1001) = 4.

For any A {0, 1}* and x {0, 1}* , the Hamming distance between x and A is

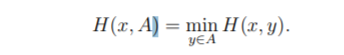
In other words, H(x, A) is the smallest number of bits we need to change in x to get a string in A.

For any A {0, 1} * , let H₂(A) = {x {0, 1} | H(x, A) 2}.

(a) Prove that if a language A is regular, then H₂(A) is also regular.

(b) Prove that if a language A is context-free, then H₂(A) is also context-free.

H(x, A) = min H(x, y). YEA