The heat conduction equation for a thin long rod is given by

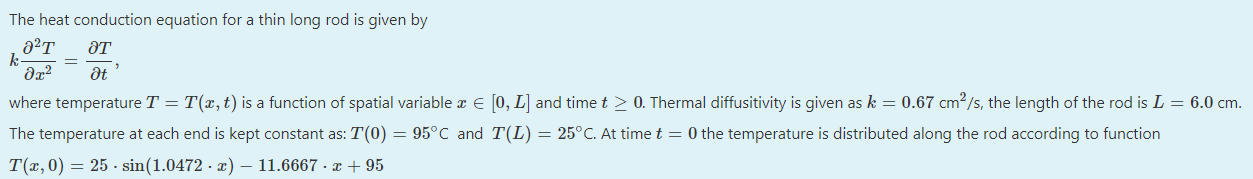
The heat conduction equation for a thin long rod is given by k- aT at where temperature T = T(x, t) is a function of spatial variable a E [0, L] and time t 2 0. Thermal diffusitivity is given as k = 0.67 cm /s, the length of the rod is L = 6.0 cm. The temperature at each end is kept constant as: T(0) = 95C and T(L) = 250C. At time t = 0 the temperature is distributed along the rod according to function T(x, 0) = 25 . sin(1.0472 . x) - 11.6667 . x + 95(b) [10 marks] Apply implicit finite difference method with Ax = 2.0cm and At = 0.1'C to evaluate temperature at points indicated in the table below. Fill in the blank spaces in the table with the values of the temperature T(x, t) at point & from the corresponding column and time instance t from the corresponding row. Round up your answers to 4 decimal places. x = 0 cmx = 2.0 cm x = 4.0 cm x = 6.0 cm t = 0s 95 25 t = 0.1 s 95 25 t = 0.2 s 95 25