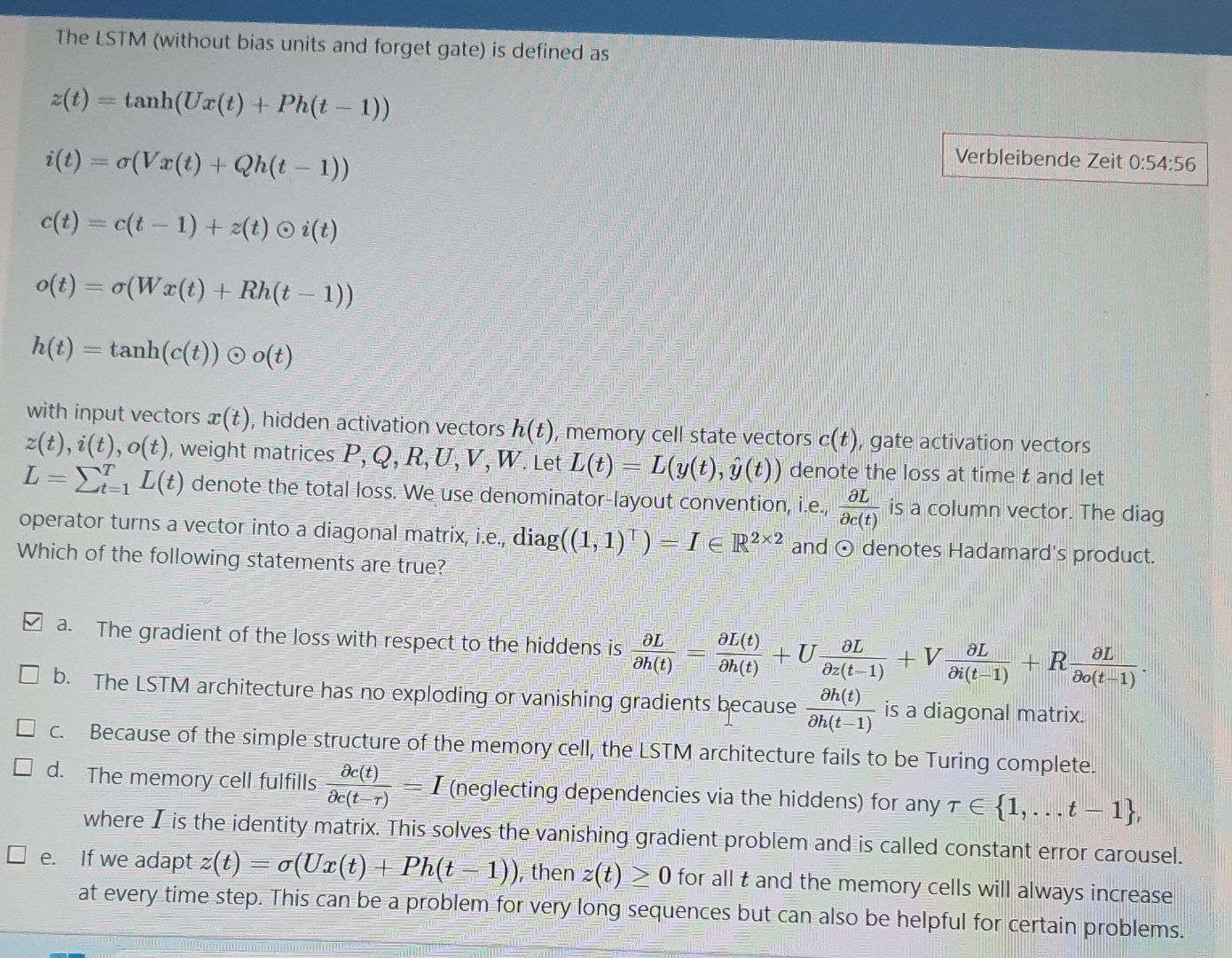
The ISTM $($without bias units and forget gate$)$ is defined as

$z(t)=tanh(Ux(t)+Ph(t-1))$

$i(t)=(Vx(t)+Qh(t-1))$

$c(t)=c(t-1)+z(t)o.i(t)$

$o(t)=(Wx(t)+Rh(t-1))$

$h(t)=tanh(c(t))o.o(t)$

Verbleibende Zeit $0$:$54$:$56$

with input vectors $x(t),$ hidden activation vectors $h(t),$ memory cell state vectors $c(t),$ gate activation vectors $z(t),i(t),o(t),$ weight matrices $P,Q,R,U,V,W.$ Let $L(t)=L(y(t),$hat$(y)(t))$ denote the loss at time $t$ and let $L={\displaystyle \underset{t=1}{\overset{T}{}}}L(t)$ denote the total loss. We use denominator$-$layout convention, i$.$e$.,\frac{\text{d}\text{e}\text{l}\text{L}}{\text{d}\text{e}\text{l}\text{c}(t)}$ is a column vector. The diag operator turns a vector into a diagonal matrix, i$.$e$.,$ diag$((1,1{)}^{TT})=Iin{R}^{22}$ and $o.$ denotes Hadamard's product. Which of the following statements are true?

a$.$ The gradient of the loss with respect to the hiddens is $\frac{\text{d}\text{e}\text{l}\text{L}}{\text{d}\text{e}\text{l}\text{h}(t)}=\frac{\text{d}\text{e}\text{l}\text{L}(t)}{\text{d}\text{e}\text{l}\text{h}(t)}+U\frac{\text{d}\text{e}\text{l}\text{L}}{\text{d}\text{e}\text{l}\text{z}(t-1)}+V\frac{\text{d}\text{e}\text{l}\text{L}}{\text{d}\text{e}\text{l}\text{i}(t-1)}+R\frac{\text{d}\text{e}\text{l}\text{L}}{\text{d}\text{e}\text{l}\text{o}(t-1)}.$

b$.$ The LSTM architecture has no exploding or vanishing gradients because $\frac{\text{d}\text{e}\text{l}\text{h}(t)}{\text{d}\text{e}\text{l}\text{h}(t-1)}$ is a diagonal matrix.

c$.$ Because of the simple structure of the memory cell, the LSTM architecture fails to be Turing complete.

d$.$ The memory cell fulfills $\frac{\text{d}\text{e}\text{l}\text{c}(t)}{\text{d}\text{e}\text{l}\text{c}(t-)}=$I $($neglecting dependencies via the hiddens$)$ for any $in\{1,$dotst$-1\},$ where I is the identity matrix. This solves the vanishing gradient problem and is called constant error carousel.

e$.$ If we adapt $z(t)=(Ux(t)+Ph(t-1)),$ then $z(t)0$ for all $t$ and the memory cells will always increase at every time step. This can be a problem for very long sequences but can also be helpful for certain problems.