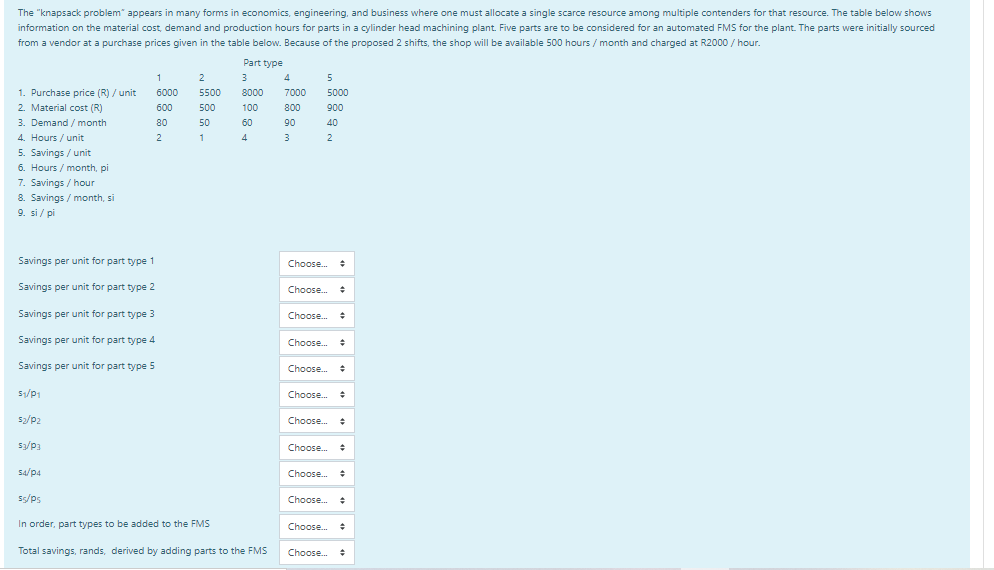
The "knapsack problem appears in many forms in economics, engineering, and business where one must allocate a single scarce resource among multiple contenders for that resource. The table below shows information on the material cost demand and production hours for parts in a cylinder head machining plant. Five parts are to be considered for an automated FMS for the plant. The parts were initially sourced from a vendor at a purchase prices given in the table below. Because of the proposed 2 shifts, the shop will be available 500 hours / month and charged at R2000 / hour. Part type 1 2 2 3 4 4 5 1. Purchase price (R) / unit ( 6000 5500 8000 7000 5000 2. Material cost(R) 600 500 100 800 900 3. Demand/month 80 50 60 90 40 4. Hours/ unit 2 1 4 3 2 5. Savings / unit 6. Hours / month, pi 7. Savings / hour 8. Savings / month, si 9. si/pi Savings per unit for part type 1 Choose... Savings per unit for part type 2 Choose... . Savings per unit for part type 3 Choose... Savings per unit for part type 4 Choose... Savings per unit for part type 5 Choose... + 51/p1 Choose.... 52/P2 Choose... . 5/pa Choose... 54/p4 Choose... s/ps Choose... In order, part types to be added to the FMS Choose... Total savings, rands, derived by adding parts to the FMS Choose.. The "knapsack problem appears in many forms in economics, engineering, and business where one must allocate a single scarce resource among multiple contenders for that resource. The table below shows information on the material cost demand and production hours for parts in a cylinder head machining plant. Five parts are to be considered for an automated FMS for the plant. The parts were initially sourced from a vendor at a purchase prices given in the table below. Because of the proposed 2 shifts, the shop will be available 500 hours / month and charged at R2000 / hour. Part type 1 2 2 3 4 4 5 1. Purchase price (R) / unit ( 6000 5500 8000 7000 5000 2. Material cost(R) 600 500 100 800 900 3. Demand/month 80 50 60 90 40 4. Hours/ unit 2 1 4 3 2 5. Savings / unit 6. Hours / month, pi 7. Savings / hour 8. Savings / month, si 9. si/pi Savings per unit for part type 1 Choose... Savings per unit for part type 2 Choose... . Savings per unit for part type 3 Choose... Savings per unit for part type 4 Choose... Savings per unit for part type 5 Choose... + 51/p1 Choose.... 52/P2 Choose... . 5/pa Choose... 54/p4 Choose... s/ps Choose... In order, part types to be added to the FMS Choose... Total savings, rands, derived by adding parts to the FMS Choose