The limit represents a derivative $f^{\text{'}}(a).$ Determine $f(x)$ and $a.$

$\underset{h0}{lim}\frac{6^h-1}{h}$

$($Express numbers in exact form. Use symbolic notation and fractions where needed.$)$

$f(x)=$

$a=$

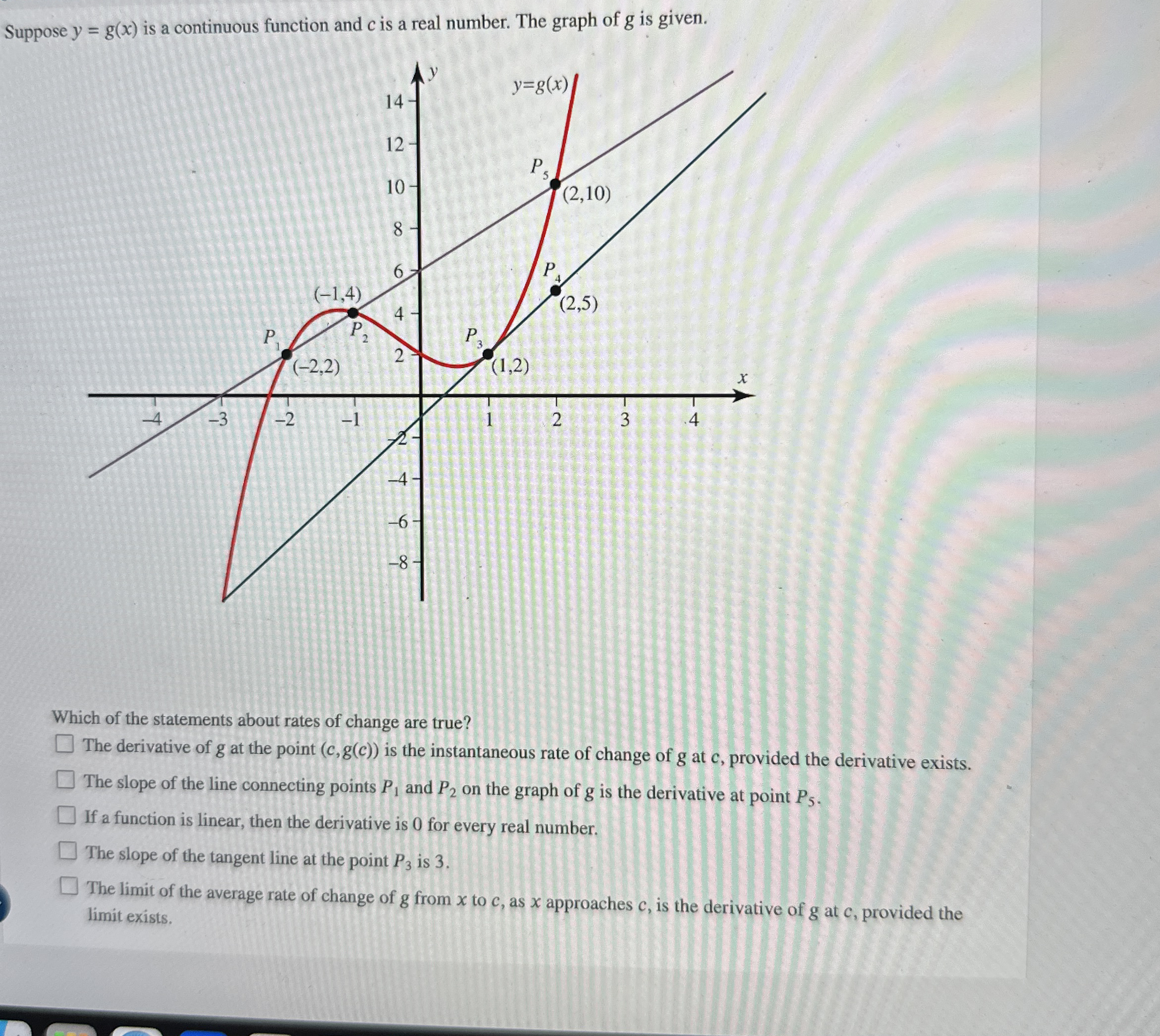
Suppose $y=g(x)$ is a continuous function and $c$ is a real number. The graph of $g$ is given.

Which of the statements about rates of change are true?

The derivative of $g$ at the point $(c,g(c))$ is the instantaneous rate of change of $g$ at $c,$ provided the derivative exists.

The slope of the line connecting points $P_1$ and $P_2$ on the graph of $g$ is the derivative at point $P_5.$

If a function is linear, then the derivative is $0$ for every real number.

The slope of the tangent line at the point $P_3$ is $3.$

The limit of the average rate of change of $g$ from $x$ to $c,$ as $x$ approaches $c,$ is the derivative of $g$ at $c,$ provided the limit exists.