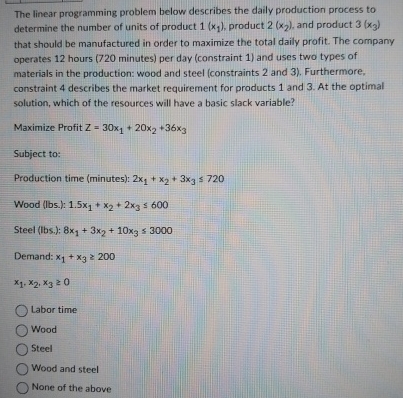
The linear programming problem below describes the daily production process to determine the number of units of product $1(x_1),$ product $2(x_2),$ and product $3(x_3)$ that should be manufactured in order to maximize the total daily profit. The company operates $12$ hours $(720$ minutes$)$ per day $($constraint $1)$ and uses two types of materials in the production: wood and steel $($constraints $2$ and $3).$ Furthermore, constraint $4$ describes the market requirement for products $1$ and $3.$ At the optimal solution, which of the resources will have a basic slack variable?

Maximize Profit $Z=30x_1+20x_2+36x_3$

Subject to:

Production time $($minutes$)$: $2x_1+x_2+3x_{3}720$

Wood $($lbs$.)$: $1\mathrm{.}5x_1+x_2+2x_{3}600$

Steel $($Ibs$.)$: $8x_1+3x_2+10x_{3}3000$

Demand: $x_1+x_{3}200$

$x_1,x_2,x_{3}0$

Labor time

Wood

Steel

Wood and steel

None of the above