Question: The loop invariant is a statement that could be proven by induction to be true before and after each iteration of the loop. So, when

The loop invariant is a statement that could be proven by

The loop invariant is a statement that could be proven by induction to be true before and after each iteration of the loop. So, when the loop terminates because p1 = 0, the loop invariant implies that the answer to the multiplication is in extra. Write a function in C that implements this pseudocode with the following header.

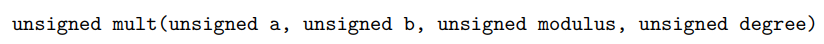induction to be true before and after each iteration of the loop. The modulus parameter will represent a polynomial of degree which will be less than 32. Parameters a and b will each represent polynomials with degree less than degree. Develop this pseudocode into a C function with the intended signature. Test it thoroughly by picking strategic inputs and comparing hand-calculated results with computer-generated results.

Let pi and p2 be elements of GF(2 n) (ie, polynomials of degree less than n) extra = 0 Loop invariant: answer to original multiplication- (p1) (p2)+extra while (p1 not o) if (pi has x0 term) p1 = p1 -X extra- extra + p2 p2 = p2 * x if (p2 has x"n term) p2 = p2 -Xn + (modulus's lower terms) Loop invariant: answer to original multiplication - (p1) (p2)+extra Let pi and p2 be elements of GF(2 n) (ie, polynomials of degree less than n) extra = 0 Loop invariant: answer to original multiplication- (p1) (p2)+extra while (p1 not o) if (pi has x0 term) p1 = p1 -X extra- extra + p2 p2 = p2 * x if (p2 has x"n term) p2 = p2 -Xn + (modulus's lower terms) Loop invariant: answer to original multiplication - (p1) (p2)+extra

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Recall the Insertion - Sort algorithm discussed in the lecture: In the lecture, you have seen a correctness proof of the algorithm based on the following loop invariant for the ( outer ) for loop:...

4. Quicksort (20 points). In practice, quicksort is one of the fastest sorting algorithms. 1. Pick a pivot (e.g. the first element) bee bed cab ace dad baa add ebb 2. Reorder the array such that all...

Answer question 2 with the format given please Q2. The following algorithm returns the product of two numbers, a and b. The parameters x and y are natural numbers. First, prove the correctness of the...

[10] Draw pictures that show the data structure each time a checkpoint is reached for the problems of sizes one, two, three and four specified as integer n_digit is the number of items in the list...

Consider this code that checks if an array is sorted in ascending order: / / Pre: array is not null / / Post: returns true if array is sorted in ascending order, false otherwise boolean isSorted (...

Consider the following function that calculates the factorial of a number: / / Pre: n > = 0 / / Post: returns the factorial of n int factorial ( int n ) { int result = 1 ; for ( int i = 1 ; i

Otis Thorpe Corporation has 10,000 shares of $100 par value, 8%, preferred stock and 50,000 shares of $10 par value common stock outstanding at December 31, 2008. Instructions Answer the questions in...

1. Is international law moving towards having more subjects? If yes, why? 2. Difference in the scope of legal personality of states and other subjects of international law? 3. Consequences of...

Cash Receipts System at S&S Context Diagram Bank Customers Cash Receipts System Management ACCT 3 1 2 Flowchart Case S&S Cash Receipts System Narrative of the S&S s cash receipts system follows:...

Problema 2 . La capacidad calor fica de un gas ideal puede expresarse como una serie de potencias en t rminos de la temperatura de acuerdo con la siguiente ecuaci n: C p = A 1 + A 2 T + A 3 T 2 + A 4...

What is the basis for Security Concerns in Cloud Computing?

Should Needs and GAP Analyses be equally applied in terms of effort when off-theshelf System Solutions being acquired versus building a custom system using Vendors or internal Programming Staff?

Describe the three main Cloud Computing Environments.