The LP problem whose output follows determines how many necklaces, bracelets, rings, and 'earrings a jewelry store should stock.

The objective function measures profit; it is assumed that every piece stocked will be sold. Constraints measure display space in units, time to set up the display in minutes and two marketing restrictions.

MAX $100N+120B+150R+125E$

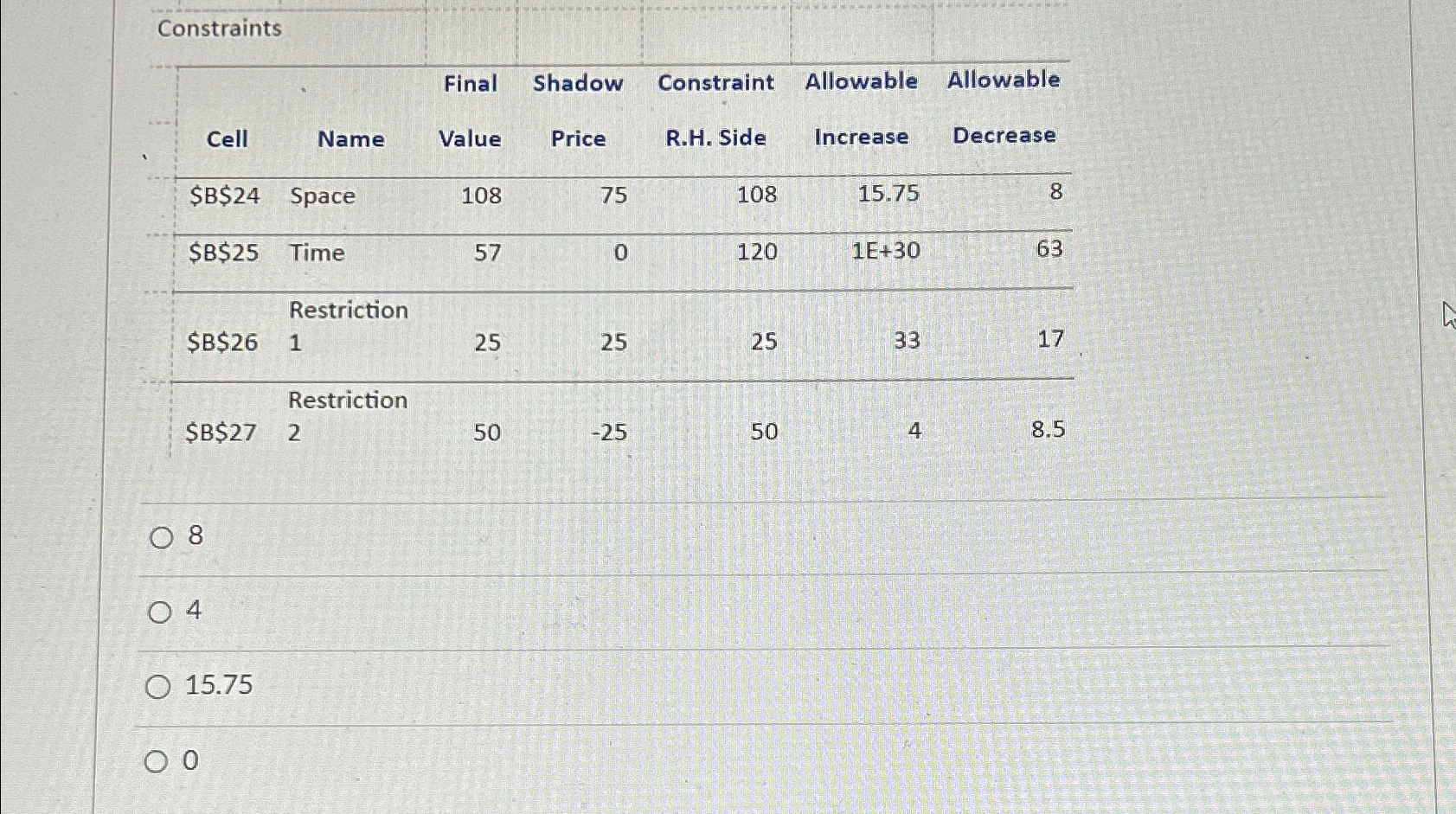
$N+2B+2R+2E<mn\; id="EditorElement\_5284207">1</mn><mn\; id="EditorElement\_5284208">0</mn><mn\; id="EditorElement\_5284209">8</mn>$ Space

$3N+5B+,E<mn\; id="EditorElement\_5284243">1</mn><mn\; id="EditorElement\_5284244">2</mn><mn\; id="EditorElement\_5284245">0</mn>$ Time

$N+R<mn\; id="EditorElement\_5284267">2</mn><mn\; id="EditorElement\_5284268">5</mn>$ Market Restriction $1$

$B+R+E>50$ Market Restriction $2$

Use the output to solve and answer the following question.

How much space will be left unused?

Variable Cells

$\backslash$table$[[$Cell$,$Name,$\backslash$table$[[$Final$],[$Value$]],\backslash$table$[[$Reduced$],[$Cost$]],\backslash$table$[[$Objective$],[$Coefficient$]],\backslash$table$[[$Allowable$],[$Increase$]],\backslash$table$[[$Allowable$],[$Decrease$]]],[$$$B$$$18,$Necklace,$8,0,100,1E+30,12\mathrm{.}5],[$$$C$$$18,$Bracelet,$0,-5,120,5,1E+30$