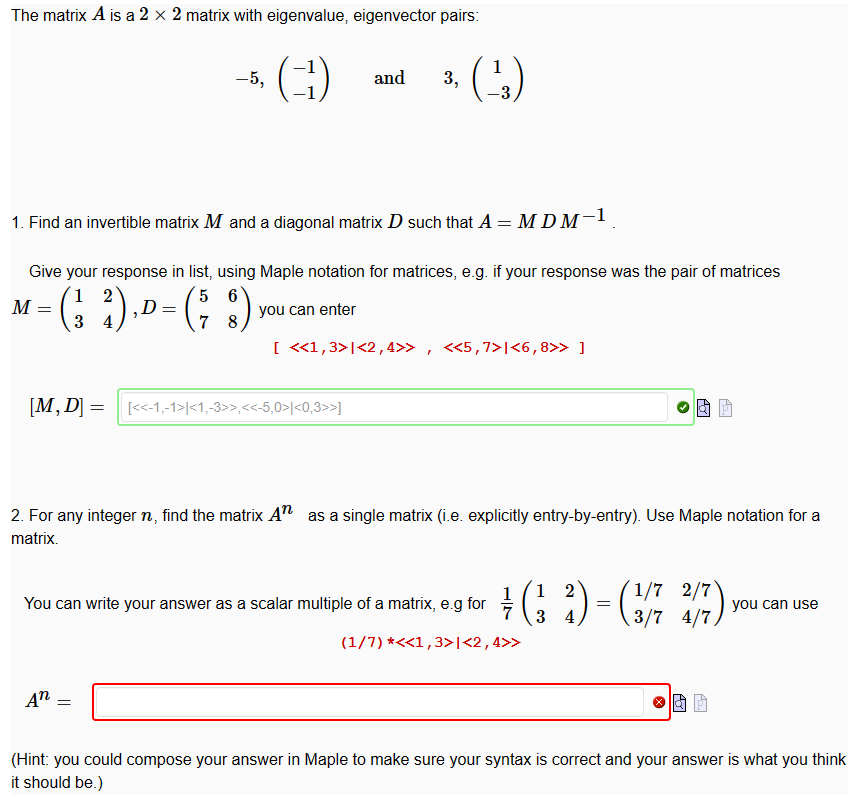
The matrix A is a 2 % 2 matrix with eigenvalue, eigenvector pairs: - (j) and 3'(13) 1. Find an invertible matrix M and a diagonal matrix D) such that A = MDM 1 Give your response in list, using Maple notation for matrices, e.g. if your response was the pair of matrices 1 2 5 6 M: D: (3 4) s (7 8) you can enter [ ]> , |> ] [M'ID]: R 2. For any integer n, find the matrix A as a single matrix (i.e. explicitly entry-by-entry). Use Maple notation for a matrix. 1/7 2/7 3/7 4/7) you can use 1 2 You can write your answer as a scalar multiple of a matrix, e.g for % (3 4) = ( (1/7) *> (Hint: you could compose your answer in Maple to make sure your syntax is correct and your answer is what you think it should be.)