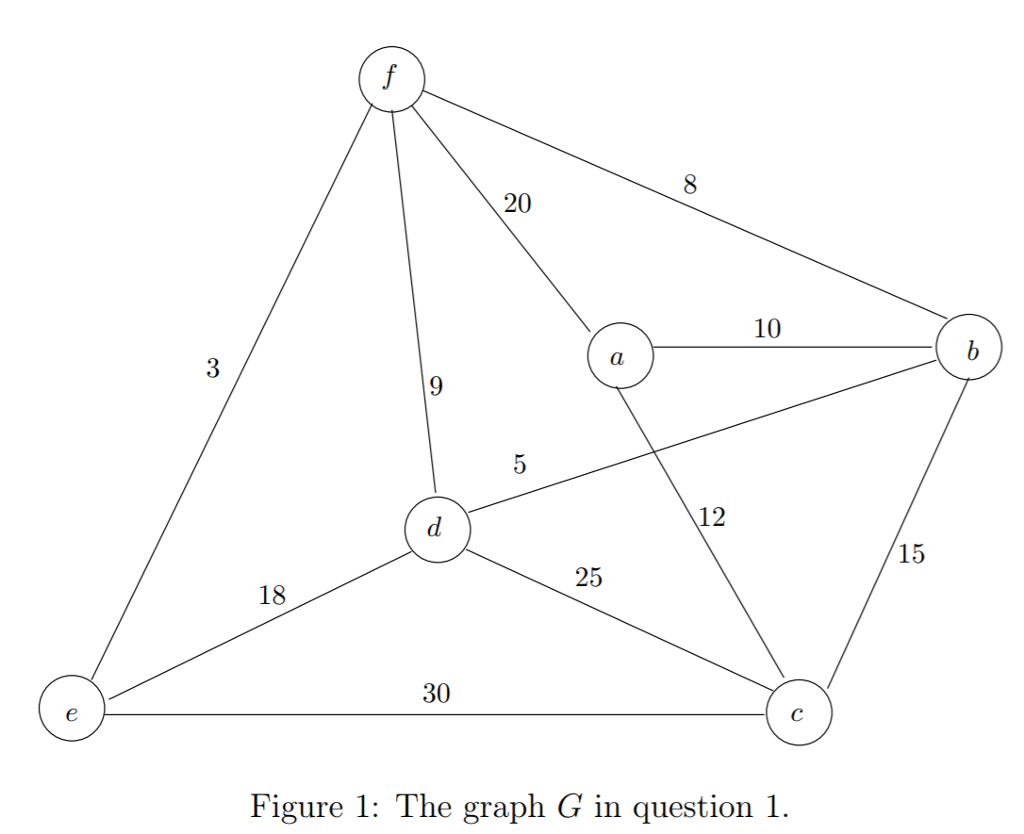
The minimum spanning tree problem is to look for a spanning tree with minimum total cost. Here, we explore another type of objective: finding a spanning tree for which the most expensive edge is as inexpensive as possible. More precisely, let G = (V, E) be a connected, undirected graph with n vertices and m edges, in which each edge is assigned a distinct weight value. Let T be a spanning tree of G.We define the jumbo edge of T to be the edge of T with the largest weight. A spanning tree T0 of G is a skinny spanning tree if there is no spanning tree of G whose jumbo edge has a smaller weight. Give a counterexample showing that not every skinny spanning tree of G must be a minimum spanning tree of the same graph. Be sure to justify your claim with adequate explanation.

Help me out this please.

20 10 9 12 15 25 18 30 Figure 1: The graph G in question1