Question: The modified Gram-Schmidt orthogonalization uses the formulas for (2) Assignment Two. Use the formulas (2) to modify the function gsqr in the script gsqr.jl into
The modified Gram-Schmidt orthogonalization uses the formulas 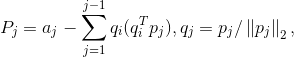 for
for 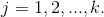 (2)
(2)
Assignment Two. Use the formulas (2) to modify the function gsqr in the script gsqr.jl into mgsqr, implementing the modified Gram-Schmidt orthogonalization method. Generate random matrices of size 20, 40, 60, 80, and 100. Apply gsqr and mgsqr on each matrix and compute the inner product of the two last vectors in the orthogonal matrix Q, as returned by gsqr and mgsqr. List these inner products in a table, using scientific format for the numbers. What do you observe about the growth of the numbers as the dimensions of the random matrices increase? Compare with the BigFloat version. Use Julia (Julia Lang)
#MCS : gsqr.jl # This script provides a simple implementation of the # Gram-Schmidt method for the QR factorization. function gsqr(A::Array{Float64,2}) # # Gram-Schmidt orthogonalization for a QR decomposition: # Q, R = gsqr(A) returns a QR decomposition of A, # computed with 64-bit floating-point arithmetic. # # ON ENTRY : # A an n-by-k Float64 matrix, n >= k. # # ON RETURN : # Q an orthogonal matrix: Q'Q = I, whose column span # is the same as the column span of A; # R an upper triangular matrix: Q*R = A. # # EXAMPLE : # a = rand(4,3); # a random 4-by-3 matrix # q, r = gsqr(a); # a - q*r # check residual # transpose(q)*q # check orthogonality # k = size(A,2) Q = deepcopy(A) R = zeros(k,k) for j = 1:k p = A[:,j] for i = 1:j-1 R[i,j] = transpose(Q[:,i])*A[:,j] p = p - Q[:,i]*R[i,j] end Q[:,j] = porm(p,2); R[j,j] = transpose(Q[:,j])*A[:,j] end return Q, R end function gsqr(A::Array{BigFloat,2}) # # Gram-Schmidt orthogonalization for a QR decomposition: # Q, R = gsqr(A) returns a QR decomposition of A, # computed with multiprecision floating-point arithmetic. # # ON ENTRY : # A an n-by-k BigFloat matrix, n >= k. # # ON RETURN : # Q an orthogonal matrix: Q'Q = I, whose column span # is the same as the column span of A; # R an upper triangular matrix: Q*R = A. # # EXAMPLE : # a = rand(4,3); # a random 4-by-3 matrix # A = Array{BigFloat,2}(a) # convert to BigFloat # q, r = gsqr(A); # A - q*r # check residual # transpose(q)*q # check orthogonality # k = size(A,2) Q = deepcopy(A) R = Array{BigFloat,2}(zeros(k,k)) for j = 1:k p = A[:,j] for i = 1:j-1 R[i,j] = transpose(Q[:,i])*A[:,j] p = p - Q[:,i]*R[i,j] end Q[:,j] = porm(p,2); R[j,j] = transpose(Q[:,j])*A[:,j] end return Q, R end function write(A::Array{Float64,2}) # # Writes the matrix is scienfic notation, # with 2 decimals after the dot, # used to print the identity matrix # to test the orthogonality of Q. # rows, cols = size(A) for i=1:rows for j=1:cols nbr = @sprintf("%+.2e", A[i,j]) print(" $nbr") end println("") end end function write(A::Array{BigFloat,2}) # # Writes the matrix is scienfic notation, # with 2 decimals after the dot, # used to print the identity matrix # to test the orthogonality of Q. # rows, cols = size(A) for i=1:rows for j=1:cols nbr = @sprintf("%+.2e", A[i,j]) print(" $nbr") end println("") end end function testFloat64() # # Generates a random 4-by-3 matrix # and tests the gsqr function # with 64-bit floating-point numbers. # a = rand(4, 3) q, r = gsqr(a) res = norm(a - q*r) stres = @sprintf("%.2e", res) println("The residual : $stres") println("Testing orthogonality, Q^T*Q is") write(transpose(q)*q) end function testBigFloat() # # Generates a random 4-by-3 matrix # and tests the gsqr function # with 64-bit floating-point numbers. # a = rand(4, 3) A = Array{BigFloat,2}(a) q, r = gsqr(A) res = norm(A - q*r,1) # no 2-norm in BigFloat on matrices stres = @sprintf("%.2e", res) println("The residual : $stres") println("Testing orthogonality, Q^T*Q is") write(transpose(q)*q) end function main() # # Runs the tests on gsqr. # testFloat64() testBigFloat() end main()##Programming Language: Julia @ Julialang
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


