The (n1) RV X has mean mX and correlation matrix RX . The RV Y is given by Y = AX + b, where A is a constant (mn) matrix and b is a constant (m1) vector. Then

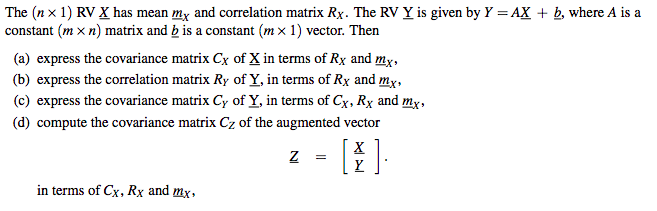
The | A* ]] RV * has mean My and correlation matrix RX . The RV' I' is given by F = AK + 6, where A is a constant I'M* A ] matrix and & is a constant I'M* 1 1 rector . Then lal express the covariance matrix CX of* in terms of Rx and My . Ibj express the correlation matrix Ry of I , in terms of RX and My . [ express the covariance matrix [ , of I , in terms of CX , Rx and my . I'd; compute the covariance matrix C & Of the augmented vector I A in terms of CX , RX and Mix