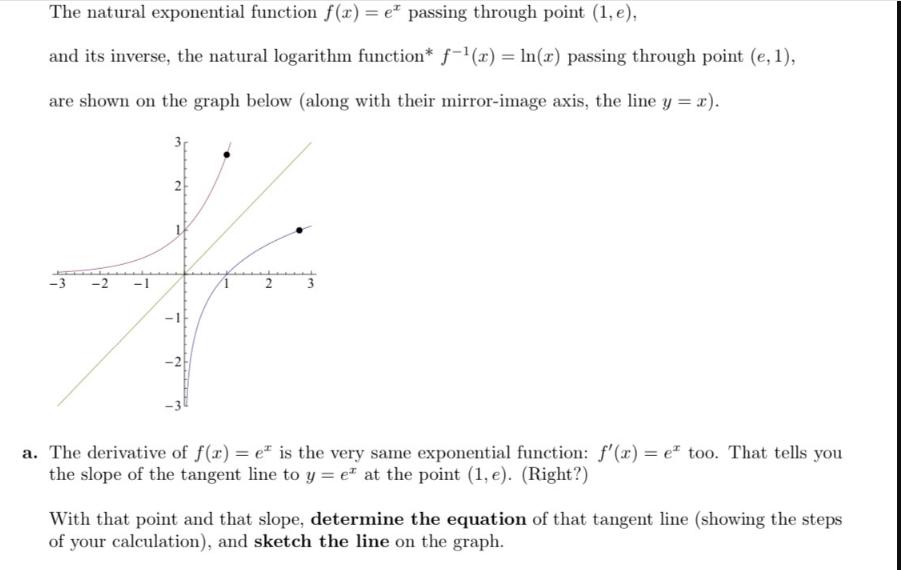
The natural exponential function f(x)= e passing through point (1, e), and its inverse, the natural logarithm function* f-(x) = ln(x) passing through point (e, 1), are shown on the graph below (along with their mirror-image axis, the line y = x). 3 2 f -2 a. The derivative of f(x) = e is the very same exponential function: f'(x) = e too. That tells you the slope of the tangent line to y = e at the point (1, e). (Right?) With that point and that slope, determine the equation of that tangent line (showing the steps of your calculation), and sketch the line on the graph. b. There's a calculus formula that states that in general, for a function f with an inverse function f- satisfying certain conditions, the inverse function's derivative is the reciprocal of the original function's derivative composed with the inverse function. (Confusing, right? Never mind, look at the formula:) 1 f'(-(x)) (-)'(x) = Now plug in ln(x) for f-(x) and e for f'(x) into that formula, and simplify the right side (showing your steps, as usual) to find an expression for the derivative of ln(r). What is it? c. That derivative tells you the slope of the tangent line to y = ln(x) at the point (e, 1). With that point and that slope, determine the equation of that tangent line (showing the steps of your calculation), and sketch the line on the graph too.