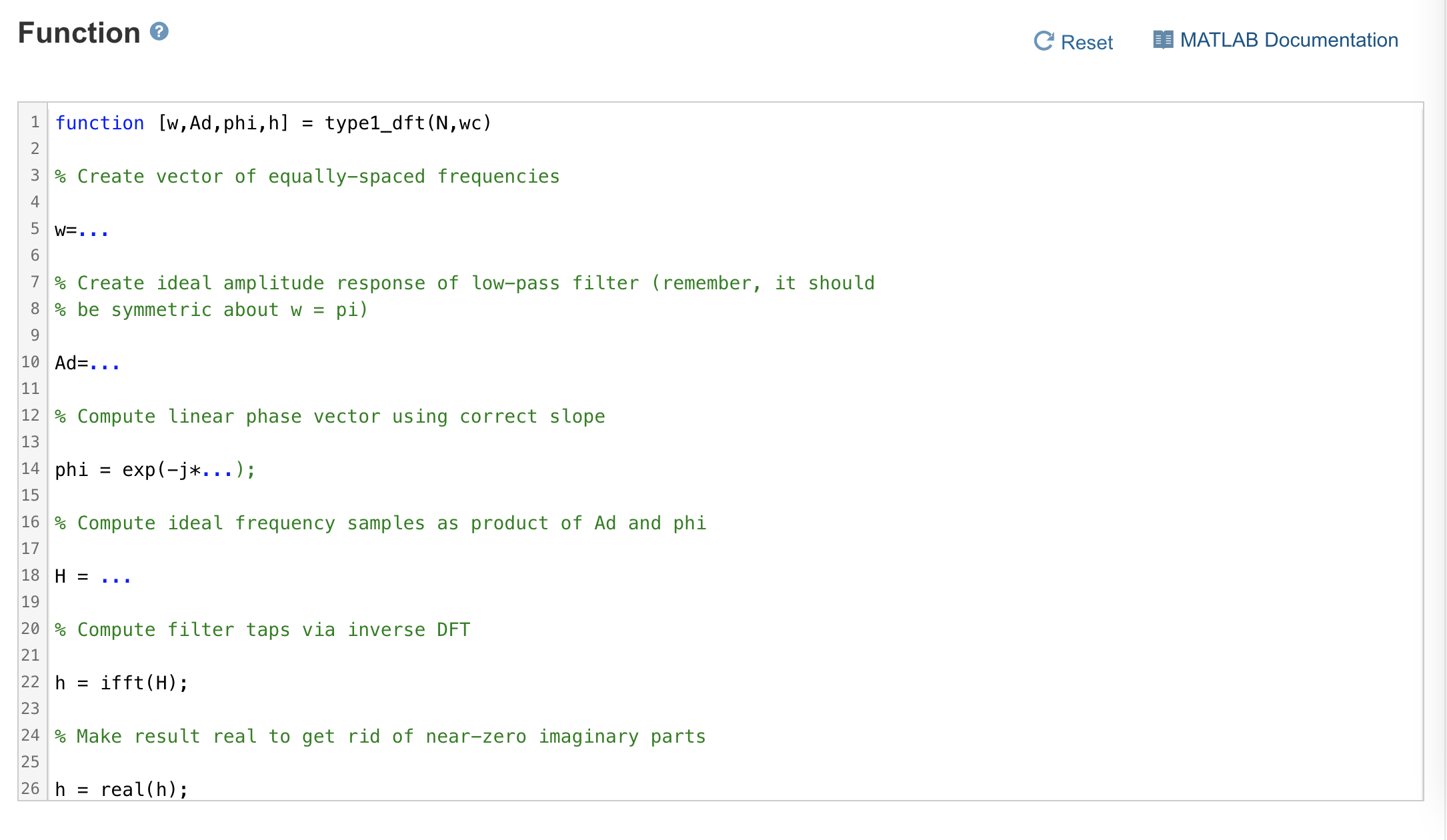
The next few problems will explore different ways of designing a Type-1 (odd length, linear phase, low-pass) FIR filter. First, write a function type1_dft that computes a filter tap vector h by determining the ideal frequency response at N equally-spaced frequencies and taking the inverse DFT of this vector. Your function should take the inputs N, an odd positive integer (>=3) w_c, a frequency cutoff in [ 0, pi) and return the outputs w, a length- N vector of equally-spaced frequency samples in [ 0, 2*pi) A_d, a length- N vector of the ideal amplitudes of a low-pass filter with cutoff w_c, corresponding to the samples in w phi, a length- N vector of the ideal phases corresponding to the samples in w (i.e., a complex vector of the form e^j(...)) h, a length- N vector of filter taps resulting from taking the inverse DFT of the frequency response samples implied by A_d and phi. I Remember that discrete-time filters must be 2*pi-periodic, and that the phase should be linear with a slope related to the filter length N. The resulting filter should be real and symmetric; you can get rid of small imaginary parts by setting h equal to real (h), but if the imaginary part is large you probably made an error. Function > 1 function [w, Ad, phi, h] 2 = 3% Create vector of equally-spaced frequencies 4 5 W... 6 7 % Create ideal amplitude response of low-pass filter (remember, it should 8% be symmetric about w = pi) 9 10 Ad=... 11 exp(-j*...); type1_dft (N, wc) 12% Compute linear phase vector using correct slope 13 14 phi = 15 16 % Compute ideal frequency samples as product of Ad and phi 17 18 H = 19 22 h = ifft (H); 23 20% Compute filter taps via inverse DFT 21 24% Make result real to get rid of near-zero imaginary parts 25 26 h = real (h); C Reset MATLAB Documentation