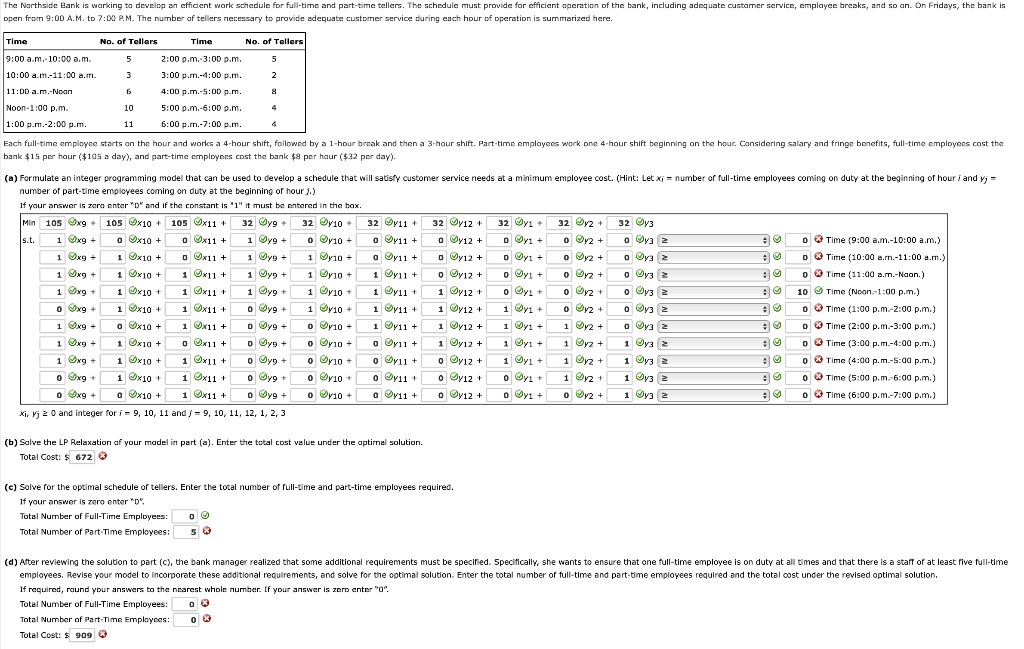
The Northside Bank is warking to develop an efficient work schedule for full-time and part-time tellers. The schedule must provide for efficient operation of the bank, including adequate customer service, emplayce breaks, and so on. On Fridays, the bank is open from 9:00 A.M. to 7:00 P.M. The number of tellers necessary to provide adequate customer service during each hour of operation is summarized here. Time No. of Tellers Time No. of Tellers 5 5 9:00 a.m. 10:00 am 10:00 am-11:00 a.m. 2:00 p.m.-3:00 p.m. 3:00 p.m.-4:00p.m. 3 2 6 8 11:DD a.m.-Noon Noon-1:00 pm 1:00p.m.-2:00 p.m. 10 4:00 p.m.-5:00p.m. 5:00 p.m.-6:00 pm 6:00 pm-7:00p.m 4 11 4 Each full-time employee starts on the hour and works a 4-hour shift, followed by a 1-hour break and then a 3-hour shift. Part-time employees work one 4-hour shift beginning on the hour. Considering salary and fringe benefits, full-time employees cost the bank $15 per hour ($105 a day), and part-time employees cost the bank $8 per haur ($32 per day). (a) Formulate an integer programming model that can be used to develop a schedule that will satisfy customer service needs at a minimum employee cost. (Hint: Let x; = number or full-time employees coming on duty at the beginning of hour i and yj = number of part-time employees coming on duty at the beginning of hour 1.) If your answer is zero entero" and if the constant is '1" it must be entered in the bax. Min 105 xg + 105 x10 + 105 x11 + 32 yg + 32 Oy10+ 32 811 + 32 Dy12 + 32 yi 32 2 + 32 y3 s.t. 1 xg + a X10 + o x11 + 1 yg + o 10+ o y11 + o 12 + o yi + o y2 + o y3 2 0 Time (9:00 a.m.-10:00 a.m.) 1 Oxg + 1 x10 + 0 x11 + 1 yg + 1 Oy10+ a y11 + o Oy12 + o Oy + o y2 + o Wy 2 0 Time (10:00a.m.-11:00a.m.) 1 xy + 1 0x10 + 1 0x11+ 1 yg + 1 Oy10+ 1 Oy11 + o y12 + o Oyl + o y2 + o y3 o Time (11:00 a.m.-Naon.) 1 x + 1 x 10+ 1 0x11+ 1 Oyg + 1 y10 + 1 v11 + 1 y12 + o Jyl + o y2 + o y3 10 Time (Noon-1:00 p.m.) 0 xg + 1 x10 + 1 x11 + o Oyo + 1 810 + 1 Ou + 1 y12 + 1 yi + o y2 + o y3 o Time (1:00 pm - 2:00 p.m.) 1 xg + a Ox10 + 1 Ox11 + o yg + o 10+ 1 711 + 1 y12 + 1 y2 + o Oy 2 0 Time (2:00 p.m.-3:00 p.m.) 1 9x19 + 0 x11 + o yg + o 10+ + a Oy11 + 1 y12 + 1 Oyl + 1 y2 + 1 ya 2 D Time (3:00 pm - 4:00 p.rn.) 1 Ang + 1 0x10 + 1 0x11+ o yg + o 10+ o Oy11 + o Oy12 + 1 Oyl + 1 y2 + 1 3 2 o Time (4:00p.m.-5:00p.m.) oxg 1 0x10 + 1 0x11 o yg + 0 Dy10+ o Oy 11 + o Dy12 oyi 1 x2 + 1 y3 2 0 Time (5:00p.m. 6:00 p.m.) 0 VNG 1 0 x10 + 1 0x11+ o yo + 0 WY10 + o Oy11 + o Oy12 + o Oyi + o 12 + i y3 2 0 Time (6:00 p.m-7:00p.m.) Xi, Vj 20 and integer for i = 9, 10, 11 and j = 9, 10, 11, 12, 1, 2, 3 (6) Salve the LP Relaxation af your model in part (a). Enter the total cost value under the aptimal solution. Total Cost: $ 672 (c) Solve for the optimal schedule of tellers. Enter the total number of full-time and part-time employees required. If your answer is zero enter " Total Nurnber of Full-Time Employees: Total Number of Part-Time Employees: 5 (d) After reviewing the solution to part (c), the bank manager realized that some additional requirements must be specified. Specifically, she wants to ensure that one full-time employee is on duty at all times and that there is a staff of at least five full-time employees. Revise your model to incorporate these additional requirements, and solve for the optimal solution. Enter the total number of full-time and part-time employees required and the total cost under the revised optimal solution. If required, round your answers to the nearest whole number. If your answer is zero enter "O". Total Number of Full-Time Employees: 03 Total Number of Part-Time Employees: 0 X Total Cost: $909 The Northside Bank is warking to develop an efficient work schedule for full-time and part-time tellers. The schedule must provide for efficient operation of the bank, including adequate customer service, emplayce breaks, and so on. On Fridays, the bank is open from 9:00 A.M. to 7:00 P.M. The number of tellers necessary to provide adequate customer service during each hour of operation is summarized here. Time No. of Tellers Time No. of Tellers 5 5 9:00 a.m. 10:00 am 10:00 am-11:00 a.m. 2:00 p.m.-3:00 p.m. 3:00 p.m.-4:00p.m. 3 2 6 8 11:DD a.m.-Noon Noon-1:00 pm 1:00p.m.-2:00 p.m. 10 4:00 p.m.-5:00p.m. 5:00 p.m.-6:00 pm 6:00 pm-7:00p.m 4 11 4 Each full-time employee starts on the hour and works a 4-hour shift, followed by a 1-hour break and then a 3-hour shift. Part-time employees work one 4-hour shift beginning on the hour. Considering salary and fringe benefits, full-time employees cost the bank $15 per hour ($105 a day), and part-time employees cost the bank $8 per haur ($32 per day). (a) Formulate an integer programming model that can be used to develop a schedule that will satisfy customer service needs at a minimum employee cost. (Hint: Let x; = number or full-time employees coming on duty at the beginning of hour i and yj = number of part-time employees coming on duty at the beginning of hour 1.) If your answer is zero entero" and if the constant is '1" it must be entered in the bax. Min 105 xg + 105 x10 + 105 x11 + 32 yg + 32 Oy10+ 32 811 + 32 Dy12 + 32 yi 32 2 + 32 y3 s.t. 1 xg + a X10 + o x11 + 1 yg + o 10+ o y11 + o 12 + o yi + o y2 + o y3 2 0 Time (9:00 a.m.-10:00 a.m.) 1 Oxg + 1 x10 + 0 x11 + 1 yg + 1 Oy10+ a y11 + o Oy12 + o Oy + o y2 + o Wy 2 0 Time (10:00a.m.-11:00a.m.) 1 xy + 1 0x10 + 1 0x11+ 1 yg + 1 Oy10+ 1 Oy11 + o y12 + o Oyl + o y2 + o y3 o Time (11:00 a.m.-Naon.) 1 x + 1 x 10+ 1 0x11+ 1 Oyg + 1 y10 + 1 v11 + 1 y12 + o Jyl + o y2 + o y3 10 Time (Noon-1:00 p.m.) 0 xg + 1 x10 + 1 x11 + o Oyo + 1 810 + 1 Ou + 1 y12 + 1 yi + o y2 + o y3 o Time (1:00 pm - 2:00 p.m.) 1 xg + a Ox10 + 1 Ox11 + o yg + o 10+ 1 711 + 1 y12 + 1 y2 + o Oy 2 0 Time (2:00 p.m.-3:00 p.m.) 1 9x19 + 0 x11 + o yg + o 10+ + a Oy11 + 1 y12 + 1 Oyl + 1 y2 + 1 ya 2 D Time (3:00 pm - 4:00 p.rn.) 1 Ang + 1 0x10 + 1 0x11+ o yg + o 10+ o Oy11 + o Oy12 + 1 Oyl + 1 y2 + 1 3 2 o Time (4:00p.m.-5:00p.m.) oxg 1 0x10 + 1 0x11 o yg + 0 Dy10+ o Oy 11 + o Dy12 oyi 1 x2 + 1 y3 2 0 Time (5:00p.m. 6:00 p.m.) 0 VNG 1 0 x10 + 1 0x11+ o yo + 0 WY10 + o Oy11 + o Oy12 + o Oyi + o 12 + i y3 2 0 Time (6:00 p.m-7:00p.m.) Xi, Vj 20 and integer for i = 9, 10, 11 and j = 9, 10, 11, 12, 1, 2, 3 (6) Salve the LP Relaxation af your model in part (a). Enter the total cost value under the aptimal solution. Total Cost: $ 672 (c) Solve for the optimal schedule of tellers. Enter the total number of full-time and part-time employees required. If your answer is zero enter " Total Nurnber of Full-Time Employees: Total Number of Part-Time Employees: 5 (d) After reviewing the solution to part (c), the bank manager realized that some additional requirements must be specified. Specifically, she wants to ensure that one full-time employee is on duty at all times and that there is a staff of at least five full-time employees. Revise your model to incorporate these additional requirements, and solve for the optimal solution. Enter the total number of full-time and part-time employees required and the total cost under the revised optimal solution. If required, round your answers to the nearest whole number. If your answer is zero enter "O". Total Number of Full-Time Employees: 03 Total Number of Part-Time Employees: 0 X Total Cost: $909