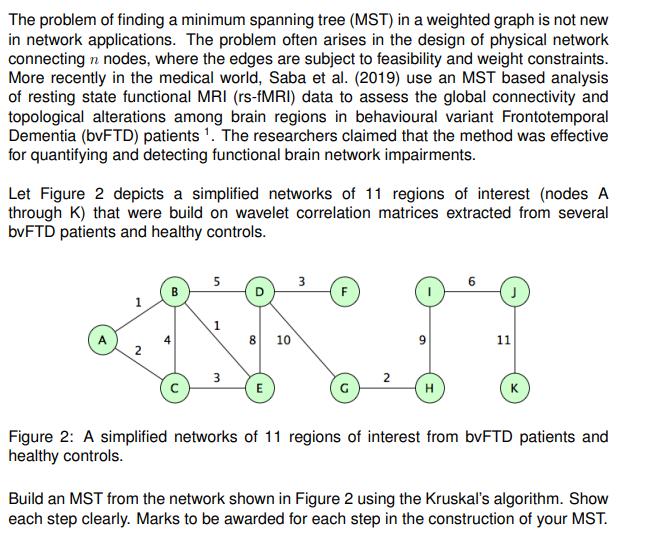
The problem of finding a minimum spanning tree (MST) in a weighted graph is not new in network applications. The problem often arises in the design of physical network connecting n nodes, where the edges are subject to feasibility and weight constraints. More recently in the medical world, Saba et al. (2019) use an MST based analysis of resting state functional MRI (rs-fMRI) data to assess the global connectivity and topological alterations among brain regions in behavioural variant Frontotemporal Dementia (bvFTD) patients 1. The researchers claimed that the method was effective for quantifying and detecting functional brain network impairments. Let Figure 2 depicts a simplified networks of 11 regions of interest (nodes A through K) that were build on wavelet correlation matrices extracted from several bvFTD patients and healthy controls. 2 1 3 8 10 E H 6 11 K Figure 2: A simplified networks of 11 regions of interest from bvFTD patients and healthy controls. Build an MST from the network shown in Figure 2 using the Kruskal's algorithm. Show each step clearly. Marks to be awarded for each step in the construction of your MST.