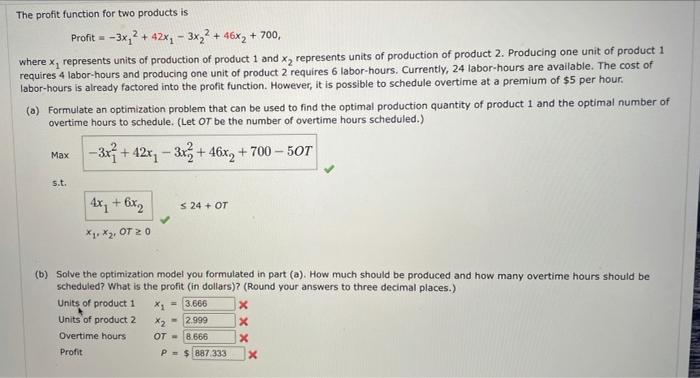
Question: The profit function for two products is Profit - -3x,2 +42x, - 3x2 + 46x2 + 700, where x, represents units of production of product
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


