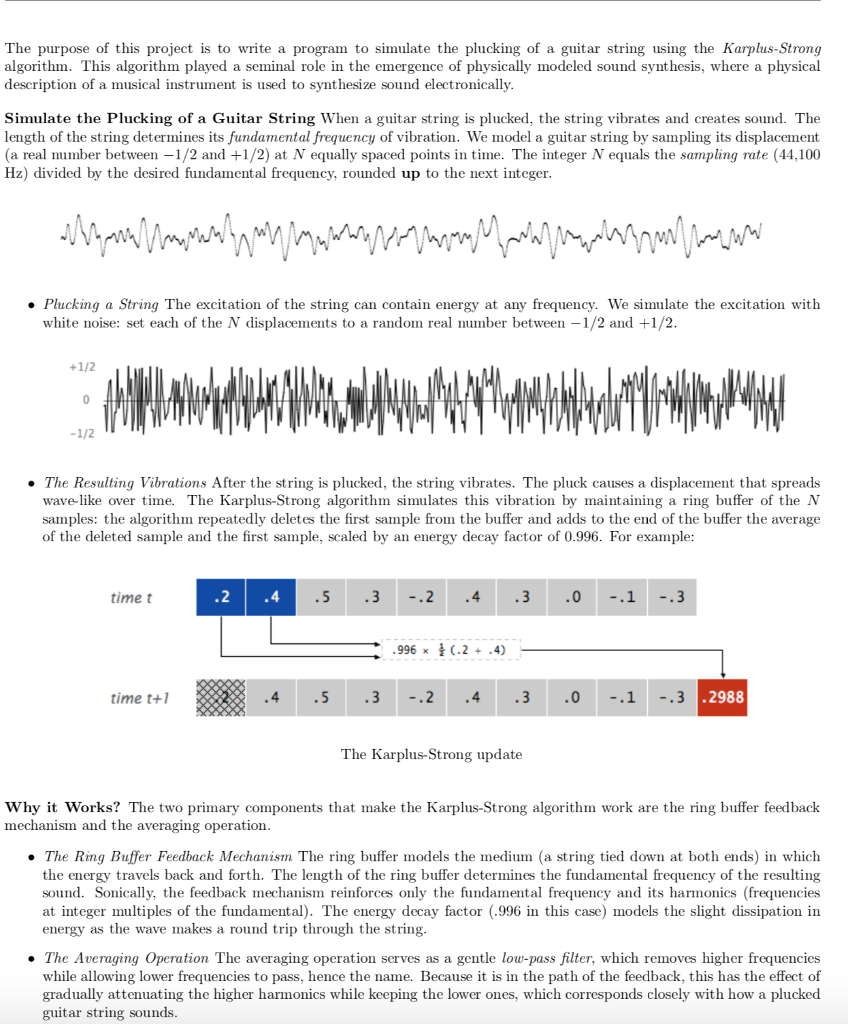
The purpose of this project is to write a program to simulate the plucking of a guitar string using the Karplus-Strong algorithm. This algorithm played a seminal role in the emergence of physically modeled sound synthesis, where a physical description of a musical instrument is used to synthesize sound electronically Simulate the Plucking of a Guitar String When a guitar string is plucked, the string vibrates and creates sound. The length of the string determines its fundamental frequency of vibration. We model a guitar string by sampling its displacement (a real number between -1/2 and +1/2) at N equally spaced points in time. The integer N equals the sampling rate (44,100 Hz) divided by the desired fundamental frequency, rounded up to the next integer Plucking a String The excitation of the string can contain energy at any frequency. We simulate the excitation with white noise: set each of the N displacements to a random real number between-1/2 and +1/2 The Resulting Vibrations After the string is plucked the string vibrates. The pluck causes a displacement that spreads wave-like over time. The Karplus-Strong algorithm simulates this vibration by maintaining a ring buffer of the N samples: the algorithm repeatedly deletes the first sample from the buffer and adds to the end of the buffer the average of the deleted sample and the first sample, scaled by an energy decay factor of 0.996. For example time t -.2.43 0 .1.3 .996 .2 + .4) time t+ .4.5 .3.2 4 .3.0-.1 -.3 2988 The Karplus-Strong update Why it Works? The two primary components that make the Karplus-Strong algorithm work are the ring buffer feedback mechanism and the averaging operation . The Ring Buffer Feedback Mechanism The ring buffer models the medium (a string tied down at both ends) in which the energy travels back and forth. The length of the ring buffer determines the fundamental frequency of the resulting sound. Sonically, the feedback mechanism reinforces only the fundamental frequency and its harmonics (frequencies at integer multiples of the fundamental). The energy decay factor (.996 in this case) models the slight dissipation in energy as the wave makes a round trip through the string . The Averaging Operation The averaging operation serves as a gentle low-pass filter, which removes higher frequencies while allowing lower frequencies to pass, hence the name. Because it is in the path of the feedback, this has the effect of gradually attenuating the higher harmonics while keeping the lower ones, which corresponds closely with how a plucked guitar string sounds The purpose of this project is to write a program to simulate the plucking of a guitar string using the Karplus-Strong algorithm. This algorithm played a seminal role in the emergence of physically modeled sound synthesis, where a physical description of a musical instrument is used to synthesize sound electronically Simulate the Plucking of a Guitar String When a guitar string is plucked, the string vibrates and creates sound. The length of the string determines its fundamental frequency of vibration. We model a guitar string by sampling its displacement (a real number between -1/2 and +1/2) at N equally spaced points in time. The integer N equals the sampling rate (44,100 Hz) divided by the desired fundamental frequency, rounded up to the next integer Plucking a String The excitation of the string can contain energy at any frequency. We simulate the excitation with white noise: set each of the N displacements to a random real number between-1/2 and +1/2 The Resulting Vibrations After the string is plucked the string vibrates. The pluck causes a displacement that spreads wave-like over time. The Karplus-Strong algorithm simulates this vibration by maintaining a ring buffer of the N samples: the algorithm repeatedly deletes the first sample from the buffer and adds to the end of the buffer the average of the deleted sample and the first sample, scaled by an energy decay factor of 0.996. For example time t -.2.43 0 .1.3 .996 .2 + .4) time t+ .4.5 .3.2 4 .3.0-.1 -.3 2988 The Karplus-Strong update Why it Works? The two primary components that make the Karplus-Strong algorithm work are the ring buffer feedback mechanism and the averaging operation . The Ring Buffer Feedback Mechanism The ring buffer models the medium (a string tied down at both ends) in which the energy travels back and forth. The length of the ring buffer determines the fundamental frequency of the resulting sound. Sonically, the feedback mechanism reinforces only the fundamental frequency and its harmonics (frequencies at integer multiples of the fundamental). The energy decay factor (.996 in this case) models the slight dissipation in energy as the wave makes a round trip through the string . The Averaging Operation The averaging operation serves as a gentle low-pass filter, which removes higher frequencies while allowing lower frequencies to pass, hence the name. Because it is in the path of the feedback, this has the effect of gradually attenuating the higher harmonics while keeping the lower ones, which corresponds closely with how a plucked guitar string sounds