The question is below

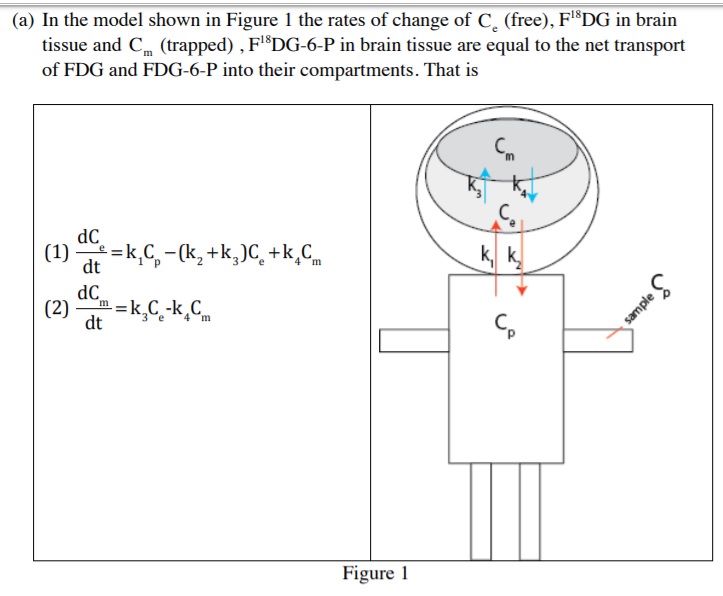
(a) In the model shown in Figure 1 the rates of change of C. (free), F"DG in brain tissue and Cm, (trapped) , F"DG-6-P in brain tissue are equal to the net transport of FDG and FDG-6-P into their compartments. That is (1) Te=k,C -(k, +k,)C+k,C k, K. dt (2) dc I'm =k.C-KC nple dt Co Figure 1where initial concentrations are assumed to be zero. Note that CF the concentration of FDG in the blood, as a function of time, is an experimentally acquired function. Then the total brain tissue concentration, Ci is given by (3} Ci = Cc + Cm Solve for Ci using the method of Laplace transforms starting with the coupled differential equations given above. Show every detail of the calculation and reproduce formula (4) in the associated paper by Brooks {Answer #1). However instead of presenting this in the form given in the paper present it in terms of convolutions (those integrals in the paper are in fact convolutions do you recognize that its also a hint). A few other hints follow: I. CP{t) is not given as an analytic function it is in fact tabulated data below. When solving this system of equations simple carry it as this symbol or its Laplace transform quantity (in [s] when appropriate. 2. I would use Cramer's rule to solve for '2'2 {5], Cm [S] 3. You may also want to use the quadratic formula to get some factors for a quadratic expression you get. 4. Remember how the convolution arises when applying the Laplace transform methodology, that is when you have a product of functions in s-spaeell