The question is left as an exercise after the lecture. Can someone help me with it?

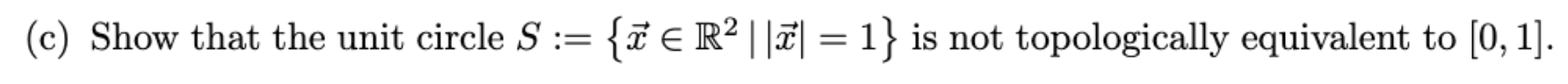
The metric space X has the fixed point property iff every continuous map f : X - X has a fixed point i.e. Ix E X st. f(x) = x. (a) Let X = [0, 1]. Show that it has the fixed point property. Hint: Intermediate value theorem. (b) Two metric spaces X and Y are topologically equivalent if there is a bijection o : X - Y which is bi-continuous, i.e. both o and - are continuous. Show that the fixed point property holds for X iff it holds for Y\f