The question is the screenshot.

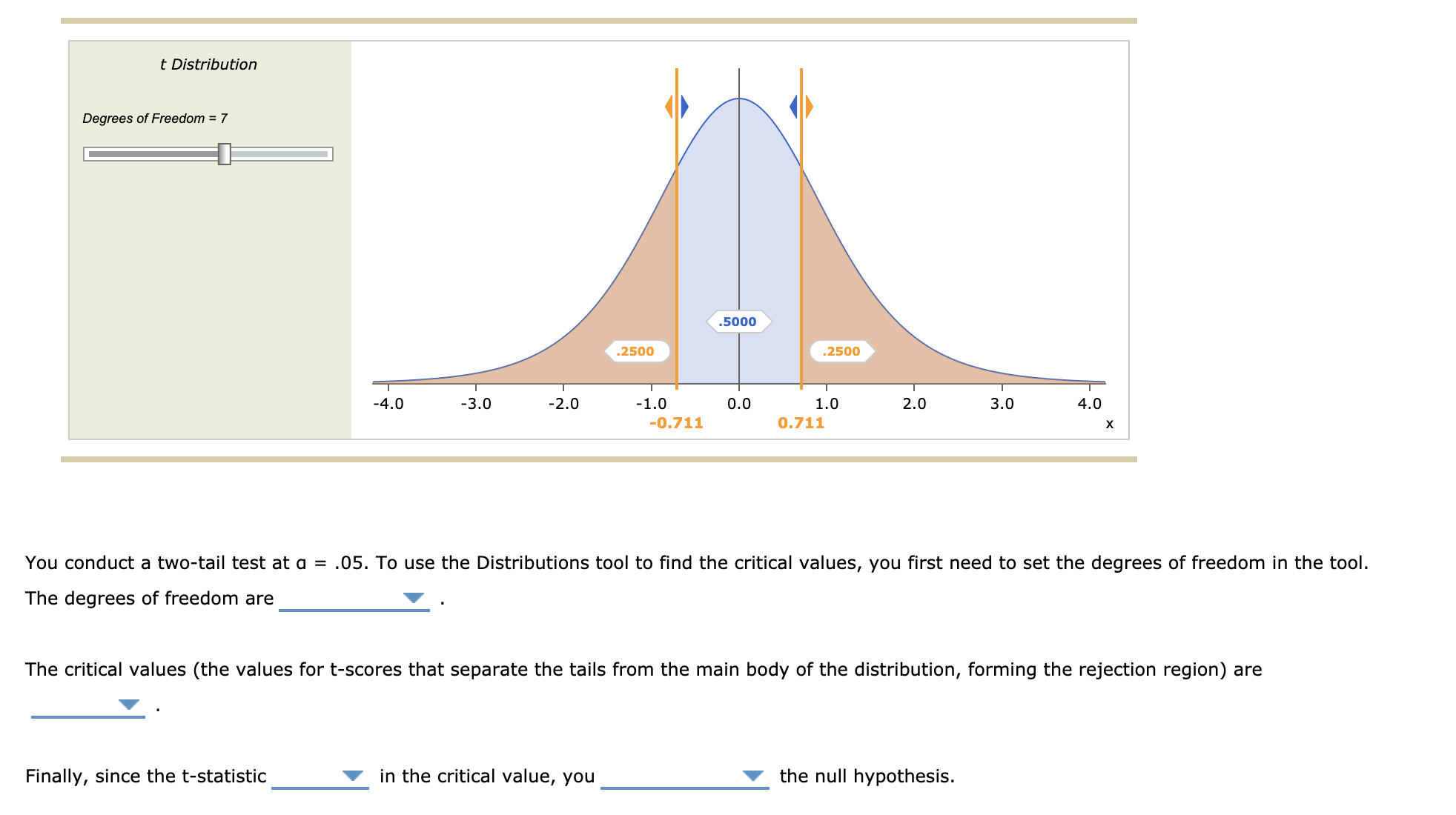
8. Calculating mean differences for matched samples Consider the following data from a matched Pairs design. You want to use a matched Pairs t-test to test the null hypothesis Ho: (1]) = 0 (the null hypothesis states that the mean difference for the general population is zero). The data consist of ve matched pairs, where the measurement from one member of the pair is labeled A, and the measurement from the other member of the pair is labeled B. Assume the population of the differences in these measurements is normally distributed. Difference Score Deviation of the Squared Deviation of Difference Score the Difference Score Observation A B (D = A - B) (D in) (D ftp)2 1 2 1 1 _V V 2 3 3 0 _v v 3 6 4 2 _V v 4 5 6 -1 _V V 5 8 6 2 _v v The mean difference score is 71]) = v Use in to complete the previous table by lling in the deviations of the difference scores and the squared deviations of the difference scores. You want to test the null hypothesis that there are no differences in means between these two matched samples (Ho: p1) = 0). To calculate the test statistic, you need to calculate the estimated standard deviation of the differences (SD). The estimated standard deviation of the differences so = v . The test statistic is t = v . t Distribution Degrees >me = 7 EEI -4.0 -3.0 V2.0 -1.0 0.0 1.0 2.0 3.0 4.0 -0.711 0.711 x You conduct a two-tail test at a = .05. To use the Distributions tool to nd the critical values, you first need to set the degrees of freedom in the tool. The degrees of freedom are v . The critical values (the values for tscores that separate the tails from the main body of the distribution, forming the rejection region) are 7 . Finally, since the t-statistic v in the critical value, you v the null hypothesis