the question needs it in labview

the question that i need help with

these are pertaining to the question

need help making the answer in labview using the program.

i need the first part of the question completed in labview formate shown in the first page.

i need help woth question 5a done in. labview and after that find the max and min force for the question above.

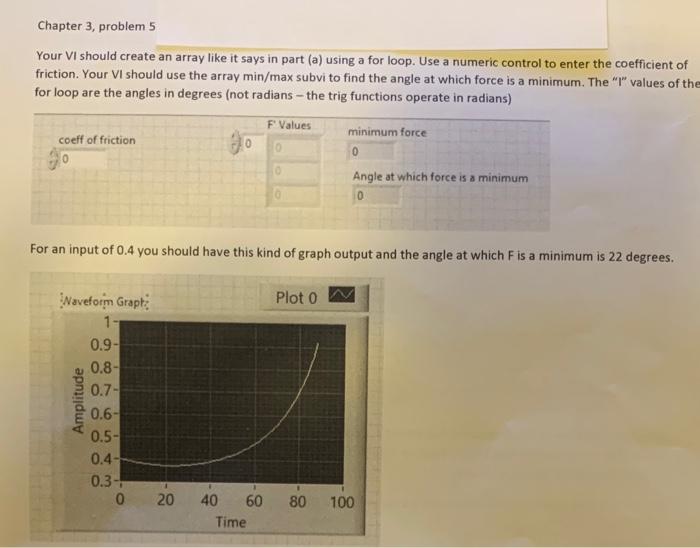
Your VI should create an array like it says in part (a) using a for loop. Use a numeric control to enter the coefficient of friction. Your VI should use the array min/max subvi to find the angle at which force is a minimum. The "I" values of the for loop are the angles in degrees (not radians - the trig functions operate in radians) For an input of 0.4 you should have this kind of graph output and the angle at which F is a minimum is 22 degrees. 5. Dragging Dresser.vi It's moving day and you are dragging a heavy dresserer constant velocity across the horizontal floor of your new apartment as SSh own in Figure 3.1. The force you are applying to the dresser has magnitude F, and it is directed at angle above the horizontal. The weight of the dresser is w, and the coefficient of kinetic friction between it and the floor is . FIG. 3.1 Problem 5. Newton's laws can be used to show that F=cos+sinW or, expressing the force as a fraction of the dresser's weight (i.e., F=F/W ), F=cos+sin (a) Write a For Loop-based program that, given from a Numeric Control labeled Coefficient of Kinetic Friction, calculates F from =0 to =90 in 1 increments and then displays the resulting array of F values on a Waveform Graph, as well as in an Array Indicator labeled Fractional Force. Suggested icons: Sine, Cosine, Degrees to Radians (this icon is only available in newer versions of LabVIEW). (b) Run your VI with =0.1,=0.4, and =1.0 and determine the angle min at which F is smallest in each case (i.e., min is the angle at which the minimum magnitude force is required to drag the dresser at constant velocity for the given )