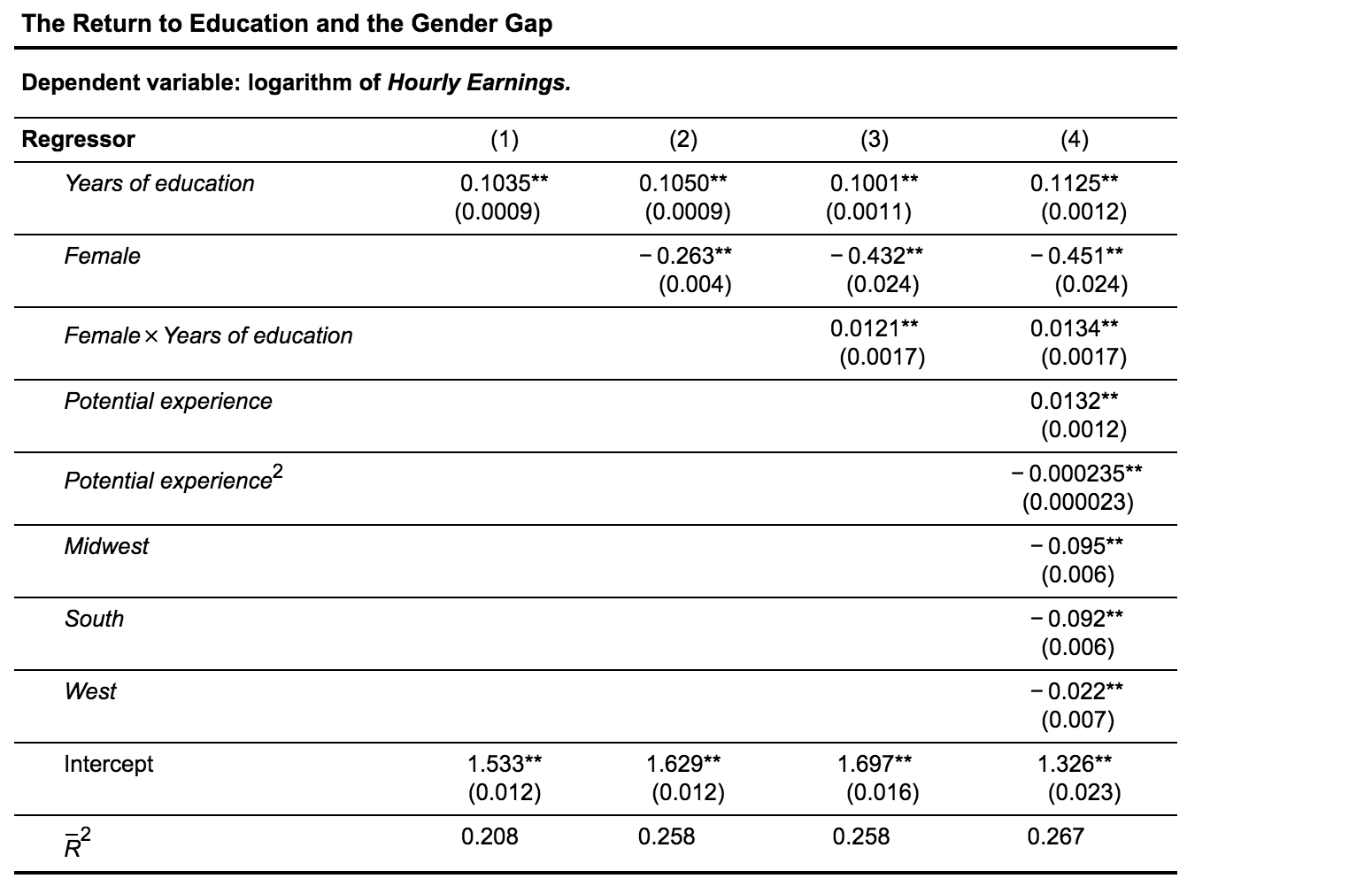
The Return to Education and the Gender Gap Dependent variable: logarithm of Hourly Earnings. Regressor (1) (3) Years of education 0.1035** (0.0009) (2) 0.1050** (0.0009) -0.263** (0.004) 0.1001** (0.0011) (4) 0.1125** (0.0012) -0.451** (0.024) Female -0.432** (0.024) Female x Years of education 0.0121** (0.0017) 0.0134** (0.0017) Potential experience 0.0132** (0.0012) Potential experience Midwest -0.000235** (0.000023) -0.095** (0.006) -0.092** (0.006) -0.022** (0.007) South West Intercept 1.533** (0.012) 1.629** (0.012) 1.697** (0.016) 1.326** (0.023) R? 0.208 0.258 0.258 0.267 Scenario A Consider a man with 18 years of education and 4 years of experience who is from a western state. Use the results from column (4) of the table and the method in Key Concept 8.1 to estimate the expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience. The expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience is %. (Round your response to two decimal places.) Scenario B Consider a man with 18 years of education and 14 years of experience who is from a western state. Use the results from column (4) of the table and the method in Key Concept 8.1 to estimate the expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience. The expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience is %. (Round your response to two decimal places.) Why are the answers to Scenario A and Scenario B different? O A. The regression is nonlinear in years of education. B. The regression is nonlinear in experience. C. The regression is nonlinear for regional variables. D. All of the above. The t-statistic for the difference between the effects in Scenario A and Scenario B is (Round your response to two decimal places.) Is the difference between the effects in Scenario A and Scenario B statistically significant at the 5% level? O A. No. B. Yes. How would you change the regression if you suspected that the effect of experience on earnings was different for men than for women? B. A. Include interaction terms Femalex Potential experience and Female x (Potential experience)2. Include interaction terms Malex Years of education and Malex (Years of education)?. Include the interaction term Female * (Years of education)2. D. Include the interaction term Malex (Years of education)?. C. The Return to Education and the Gender Gap Dependent variable: logarithm of Hourly Earnings. Regressor (1) (3) Years of education 0.1035** (0.0009) (2) 0.1050** (0.0009) -0.263** (0.004) 0.1001** (0.0011) (4) 0.1125** (0.0012) -0.451** (0.024) Female -0.432** (0.024) Female x Years of education 0.0121** (0.0017) 0.0134** (0.0017) Potential experience 0.0132** (0.0012) Potential experience Midwest -0.000235** (0.000023) -0.095** (0.006) -0.092** (0.006) -0.022** (0.007) South West Intercept 1.533** (0.012) 1.629** (0.012) 1.697** (0.016) 1.326** (0.023) R? 0.208 0.258 0.258 0.267 Scenario A Consider a man with 18 years of education and 4 years of experience who is from a western state. Use the results from column (4) of the table and the method in Key Concept 8.1 to estimate the expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience. The expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience is %. (Round your response to two decimal places.) Scenario B Consider a man with 18 years of education and 14 years of experience who is from a western state. Use the results from column (4) of the table and the method in Key Concept 8.1 to estimate the expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience. The expected change in the logarithm of average hourly earnings (AHE) associated with an additional year of experience is %. (Round your response to two decimal places.) Why are the answers to Scenario A and Scenario B different? O A. The regression is nonlinear in years of education. B. The regression is nonlinear in experience. C. The regression is nonlinear for regional variables. D. All of the above. The t-statistic for the difference between the effects in Scenario A and Scenario B is (Round your response to two decimal places.) Is the difference between the effects in Scenario A and Scenario B statistically significant at the 5% level? O A. No. B. Yes. How would you change the regression if you suspected that the effect of experience on earnings was different for men than for women? B. A. Include interaction terms Femalex Potential experience and Female x (Potential experience)2. Include interaction terms Malex Years of education and Malex (Years of education)?. Include the interaction term Female * (Years of education)2. D. Include the interaction term Malex (Years of education)?. C