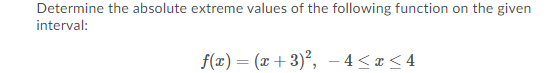
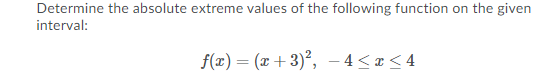
The second derivative of the position function is the acceleration function. t. a t O True FalseOn Jupiter, when an object is launched vertically from ground level with an initial velocity of 50 m/s, its position after t seconds is given by s (t) = 50t - 7+2 metres above ground level. 1. When does the object stop rising? 2. What is its maximum height? 3. What is the acceleration of the object?Determine the absolute extreme values of the following function on the given interval: f(x) = (x+3) , -4