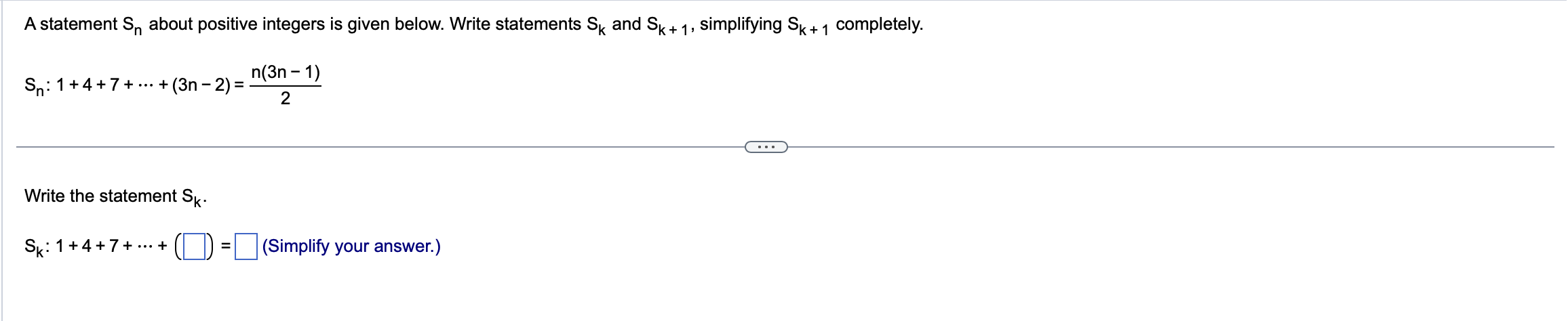
The sequence shown below is defined using a recursion formula. Write the first four terms of the sequence. a1 = 2 and an = an - 1 + 4 for n 2 2 a =Write the first four terms of the sequence whose general term is given below. an = 6(n + 1)! .. a1 =Use the formula for the general term (the nth term) of an arithmetic sequence to find the 50th term of the sequence with the given first term and common difference. a1 =4; d = 3 a50 =Find the sum of the first 50 terms of the arithmetic sequence below. - 16, -11, -6, -1, ... . . . The sum isFind the sum of the even integers between 25 and 55. The sum is Use the formula for the general term (the nth term) of a geometric sequence to find the indicated term of the following sequence with the given first term, a, , and common ratio, r. Find a14 when a, = 6 and r= - 4. . . . a14 = (Type an integer or a decimal.)Find the sum of the first 13 terms of the geometric sequence shown below. 5 2 5, - 10, 20, ... The sum of the first 13 terms is . (Round to two decimal places as needed.)Find the fourth term in the expansion of (x 3)7. The fourth term is . (Simplify your answer.) Find the term of the binomial expansion containing y16. (x3 + y) 23 The term of the binomial expansion containing y16 is (Simplify your answer.) A statement S about the positive integers is given below. Write statements Sk and Sk + 1. S: 5+ 11 +17 + ... + (6n -1) = n(3n +2) SK: 5 + 11 +17 + ...+ (6k -1) =A statement S about positive integers is given below. Write statements Sk and Sk + 1, simplifying Sk + 1 completely. Sn: 1+4+7+ ... +(3n -2) = n(3n -1) 2 . . . Write the statement Sk- SK: 1+4+7 + ...+ ( =(Simplify your answer.)