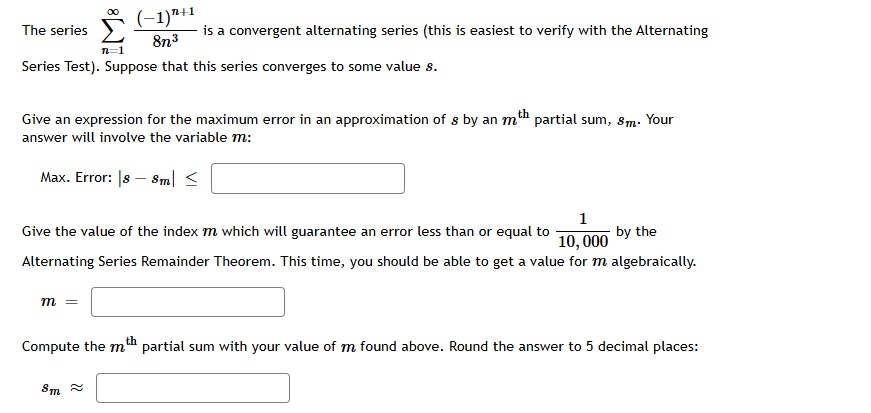
Question: The series sum _ ( n = 1 ) ^ ( infty ) ( ( - 1 ) ^ ( n + 1
The series sumninfty nn is a convergent alternating series this is easiest to verify with the Alternating
Series Test Suppose that this series converges to some value s
Give an expression for the maximum error in an approximation of s by an mth partial sum, sm Your
answer will involve the variable m :
Max. Error: ssm
Give the value of the index m which will guarantee an error less than or equal to by the
Alternating Series Remainder Theorem. This time, you should be able to get a value for m algebraically.
m
Compute the mth partial sum with your value of m found above. Round the answer to decimal places:
sm~~
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


