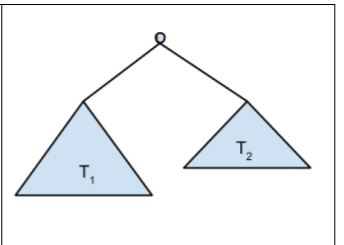
The set of full binary trees is defined recursively: Basis step: The tree consisting of a single vertex is a full binary tree. Recursive step: If T1 and T2 are disjoint full binary trees, there is a full binary tree, denoted by T1 T2, consisting of a root r together with edges connecting r to each of the roots of the left subtree T1 and the right subtree T2. Use structural induction to show that l(T), the number of leaves of a full binary tree T, is 1 more than i(T), the number of internal vertices of T

2