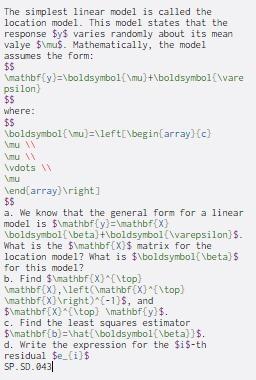
The simplest linear model is called the location model. This model states that the response $y$ varies randomly about its mean valye $\mus. Mathematically, the model assumes the form: $$ mathbf{y}=\boldsymbol[\mu}+\boldsymbol[/vare psilon $$ where: $$ boldsymbol{\mu)=\left\begin{array}{c} Imu mu \dots mu \end{array} ight 1 $$ a. We know that the general form for a linear model is $\mathbf {y}=\mathbf [X] \boldsymbol[\beta) +\boldsymbol(\varepsilon}$. What is the $\mathbf[X]$ matrix for the location model? What is $\boldsymbol[\beta] $ for this model? b. Find $\mathbf {X}^{\top] \mathbfcx), \left\mathbfEX)*[\top! \mathbfEX] ight)^{-1}$, and $\mathbf {x^{\top) \mathbf {y]$. c. Find the least squares estimator $\mathbf {b}=\hat [boldsymbol[beta]$. d. Write the expression for the $i$-th residual $e_{i}$ SP.SD.0431