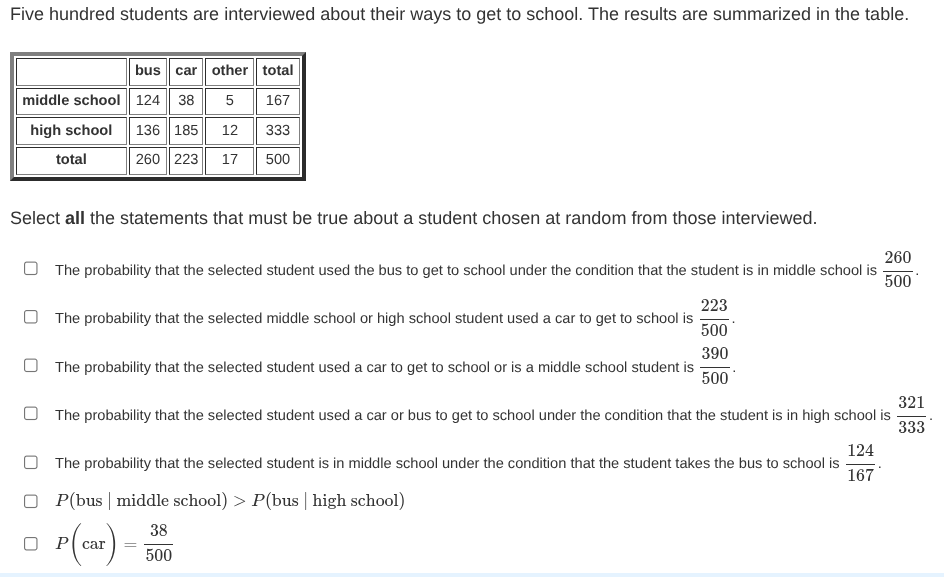
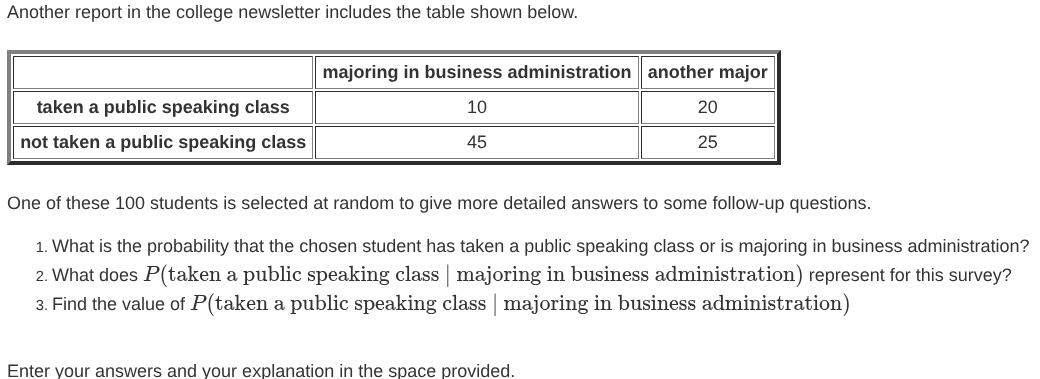
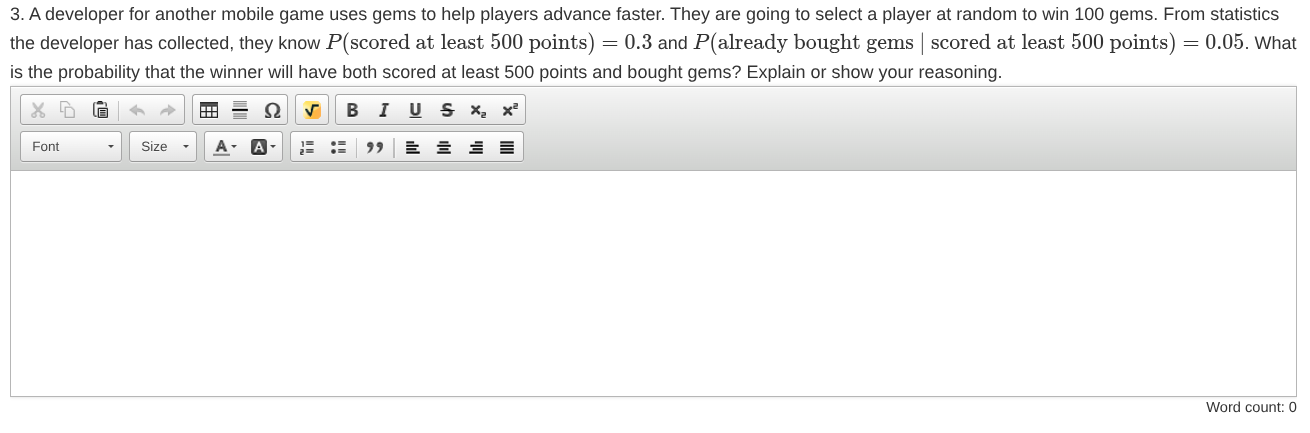
The table shows the seasons when 7 different students play a sport. fall sport || winter sport || spring sport student 1 x student 2 student 3 student 4 student 5 student 6 student 7 One of these seven students will be selected at random. Which of these events describes students 1, 4, 5, 6, and 7 without including any of the other students? . Plays a fall sport or a spring sport . Plays a fall sport and a spring sport . Plays a fall sport and not a winter sport Oo Does not play a winter sport Five hundred students are interviewed about their ways to get to school. The results are summarized in the table. bus middle school || 124 high school | 136 total 260 Select all the statements that must be true about a student chosen at random from those interviewed. 260 _} The probability that the selected student used the bus to get to school under the condition that the student is in middle school is 500" (1 The probability that the selected middle school or high school student used a car to get to school is 500 390 |} The probability that the selected student used a car to get to school or is a middle school student is . 500 _ +. 7 ae _ 32 L) The probability that the selected student used a car or bus to get to school under the condition that the student is in high school is 333 124 The probability that the selected student is in middle schoo! under the condition that the student takes the bus to school is eT" P(bus | middle school) > P(bus | high school) OP _ car) = 559 Select all the statements or equations that show that events A and B are independent. O P(A and B) = P(A) . P(B) O P(A or B) = P(A) + P(B) - P(A and B) P(A | B) = P(A) and P(B | A) = P(B) O P(A ) is the same whether event B happens or not. P(A and B) OPAB P(A)Areport in the college newsletter used the registrar's database for all the students in the school to look at majors and classes being taken this semester. The report includes the sentences: - \"One-fifth of the students at the school are taking a science class this semester.\" + \"Aquarter of the students at the school are majoring in English.\" - \"Three hundred of the 6,000 students at the school are English majors taking science classes.\" For a follow-up story, a reporter plans to visit a science class and select a student at random in the class to interview. Is there enough information from the original story to find the probability that the selected student in the science class is an English major? If so, find the probability and show your reasoning. If not, what additional information from the original report would help to find the probability? Enter your answers and your explanation in the space provided. Another report in the college newsletter includes the table shown below. majoring in business administration | another major taken a public speaking class 10 | 20 not taken a public speaking class 45 | 25 One of these 100 students is selected at random to give more detailed answers to some follow-up questions. 1. What is the probability that the chosen student has taken a public speaking class or is majoring in business administration? 2.What does P(taken a public speaking class | majoring in business administration) represent for this survey? 3. Find the value of P(taken a public speaking class | majoring in business administration) Enter your answers and your explanation in the space provided. Shrimp are often found in tropical climates and can be raised on farms or caught in the wild. Elena was taking inventory of 1-pound shrimp packages at the end of the day at a seafood market. She recorded the country of origin and whether the package contained shrimp that were farm-raised or wild-caught. . 27 packages of shrimp were farm-raised in Mexico. . 40 packages of shrimp were farm-raised in Honduras. . 52 packages of shrimp were farm-raised in Ecuador. . 13 packages of shrimp were wild-caught in Mexico. . 6 packages of shrimp were wild-caught in Honduras. . 28 packages of shrimp were wild-caught in Ecuador. 1. Construct a two-way frequency table to summarize the data based on country of origin and whether the shrimp were wild-caught or farm-raised. 2. A package of shrimp is selected at random from those inventoried. Are the events "wild-caught" and "came from Honduras" independent? Explain your reasoning. Enter your answers and your explanation in the space provided. You may also use the drawing tool to help explain or support your answer.A mobile game designer is curious about people buying additional coins in the game to progress through the levels in the game. After a beta test including 100 players, the designer determined the probability that a randomly chosen beta tester played fewer than 3 hours per week and purchased fewer than 10 coins is 0.45. played fewer than 3 hours per week || played more than 3 hours per week purchased fewer than 10 coins 0.45 purchased at least 10 coins 1. Among the beta testers, 45 of them played fewer than 3 hours per week and purchased fewer than 10 coins. Describe the group of people represented by the remaining 55 beta testers. Enter your answers and your explanation in the space provided. 2. The probability that a randomly chosen beta tester purchased fewer than 10 coins is 0.6. The probability that a randomly chosen beta tester spent greater than 3 hours per week on the game is 0.25. Use these values to complete the table. Select color played fewer played more than 3 hours per than 3 hours per week week purchased fewer than 10 coins Select size - purchased at r least 10 coins O Oe. | Eraser Clear All 3. A developer for another mobile game uses gems to help players advance faster. They are going to select a player at random to win 100 gems. From statistics the developer has collected, they know P(scored at least 500 points) = 0.3 and P(already bought gems | scored at least 500 points) = 0.05. What is the probability that the winner will have both scored at least 500 points and bought gems? Explain or show your reasoning. V BIUSX X Font Size A . A Word count: 0