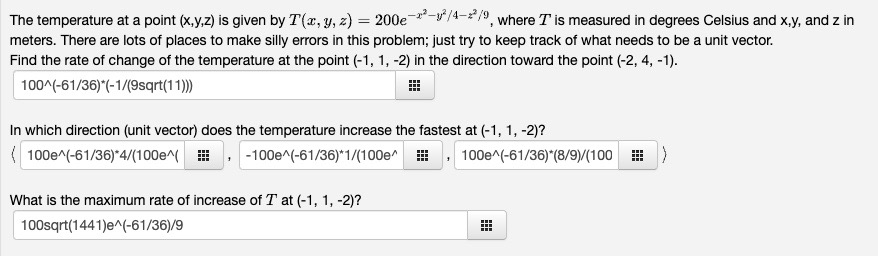
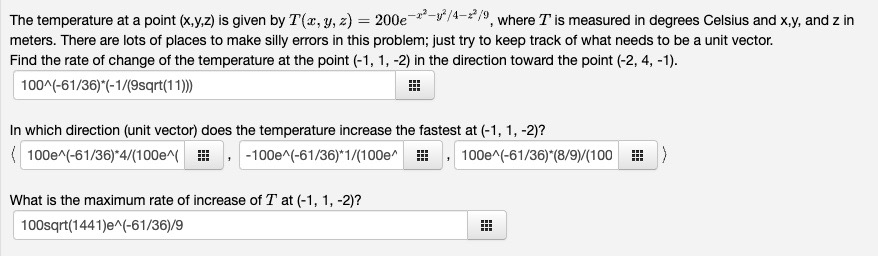
The temperature at a point (x,y,z) is given by T(x, y, z) = 200e -/4-/3, where T is measured in degrees Celsius and x,y, and z in meters. There are lots of places to make silly errors in this problem; just try to keep track of what needs to be a unit vector. Find the rate of change of the temperature at the point (-1, 1, -2) in the direction toward the point (-2, 4, -1). 100^(-61/36)*(-1/(9sqrt(11))) In which direction (unit vector) does the temperature increase the fastest at (-1, 1, -2)? 100e^(-61/36)*4/(100em( -100e^(-61/36)*1/(100e* 100e^(-61/36)*(8/9)/(100 What is the maximum rate of increase of T at (-1, 1, -2)? 100sqrt(1441)e^(-61/36)/9