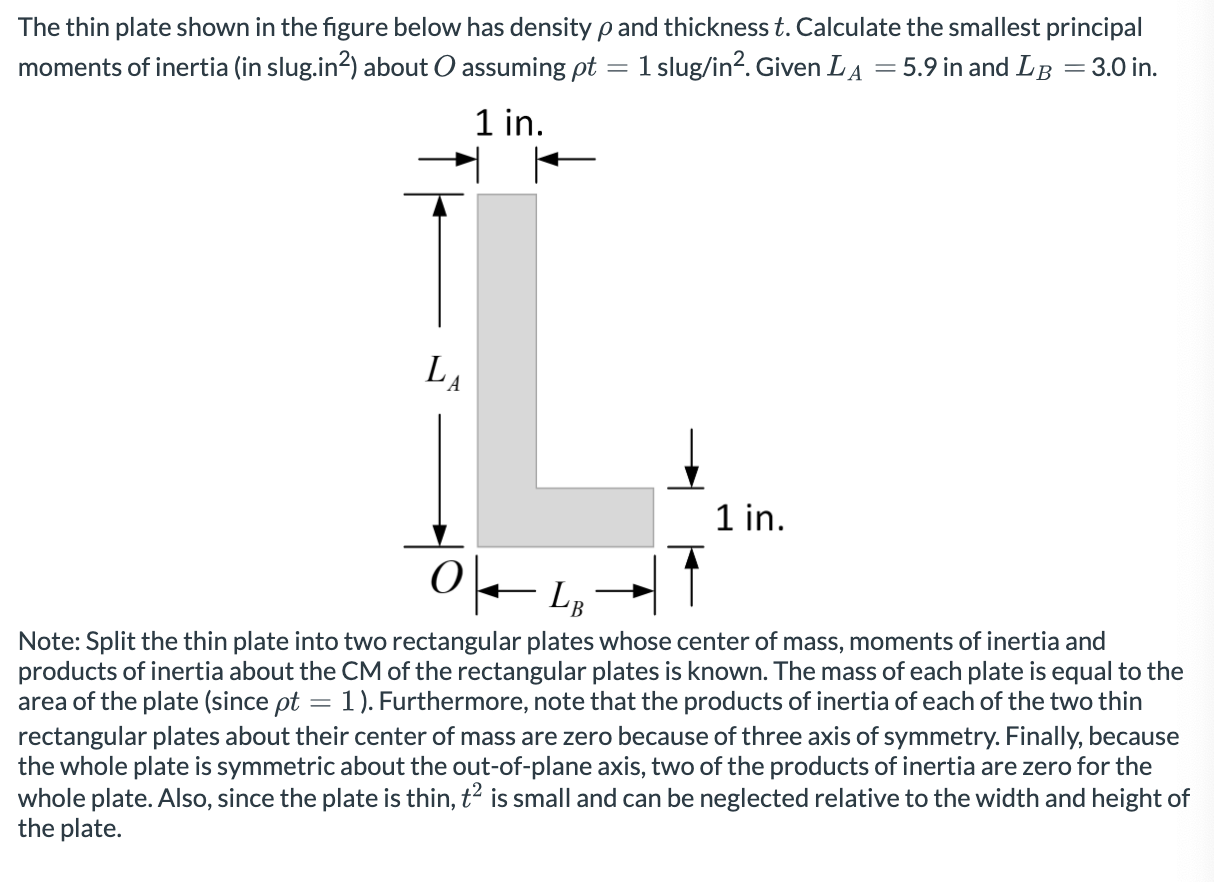
Question: The thin plate shown in the figure below has density ( rho ) and thickness ( t ) . Calculate
The thin plate shown in the figure below has density rho and thickness t Calculate the smallest principal moments of inertia in slug.in about O assuming rho t slugmathrmin Given LA in and LBmathrmin
Note: Split the thin plate into two rectangular plates whose center of mass, moments of inertia and products of inertia about the CM of the rectangular plates is known. The mass of each plate is equal to the area of the plate since rho t Furthermore, note that the products of inertia of each of the two thin rectangular plates about their center of mass are zero because of three axis of symmetry. Finally, because the whole plate is symmetric about the outofplane axis, two of the products of inertia are zero for the whole plate. Also, since the plate is thin, t is small and can be neglected relative to the width and height of the plate.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


