The three allocation methods (i) Equal allocation (ii) Proportional allocation (iii) Neumann allocation

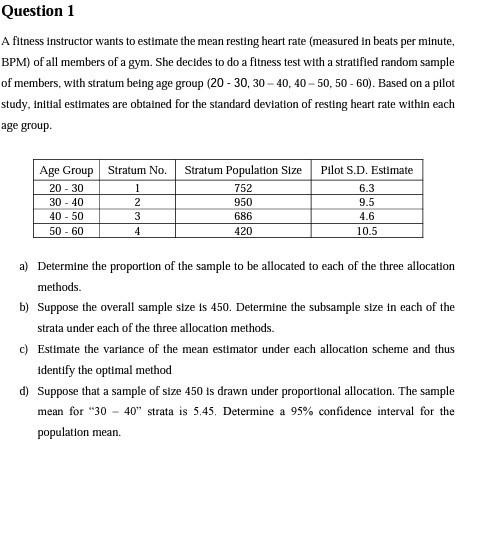
Question 2 A youth development organisation wishes to estimate the proportion of secondary schools in the Western Cape that offer online classes. They decide to stratify by school ownership (state vs. private). Stratum population sizes are displayed below, along with the results of a pilot survey conducted with 50 state schools and 10 private schools. School Ownership State Private Stratim 1 2 Stratum Population Size 1200 800 Pilot Proportion Estimate 0.35 0.73 a) Determine the proportion of the sample to be allocated to each stratum under (1) equal allocation: (11) proportional allocation; () Neyman allocation. b) Suppose the overall sample size is 500. Determine the subsample size in each of the strata under each of the three allocation methods. C) Estimate the variance of the proportion estimator under each of the three allocation methods, as well as under SRS. Which method appears to be best? d) Suppose that a sample of size 300 is drawn under Neyman allocation. The sample proportions in the two strata are respectively 0.24 and 0.71. Determine (t) the overall proportion estimate. (lt) an improved estimate of the variance of the proportion estimator, and (lit) a 95% confidence interval for the population proportion. Question 1 A fitness instructor wants to estimate the mean resting heart rate (measured in beats per minute, BPM) of all members of a gym. She decides to do a fitness test with a stratified random sample of members, with stratum being age group (20-30, 30-40, 40-50, 50 - 60). Based on a pilot study, initial estimates are obtained for the standard deviation of resting heart rate within each age group. Age Group Stratum No. 20 - 30 1 30 - 40 2 40 - 50 3 50 - 60 4 Stratum Population Size 752 950 686 420 Pilot S.D. Estimate 6.3 9.5 4.6 10.5 a) Determine the proportion of the sample to be allocated to each of the three allocation methods. b) Suppose the overall sample size is 450. Determine the subsample size in each of the strata under each of the three allocation methods. c) Estimate the variance of the mean estimator under each allocation scheme and thus identify the optimal method d) Suppose that a sample of size 450 is drawn under proportional allocation. The sample mean for "30 - 40" strata is 5.45. Determine a 95% confidence interval for the population mean. Question 2 A youth development organisation wishes to estimate the proportion of secondary schools in the Western Cape that offer online classes. They decide to stratify by school ownership (state vs. private). Stratum population sizes are displayed below, along with the results of a pilot survey conducted with 50 state schools and 10 private schools. School Ownership State Private Stratim 1 2 Stratum Population Size 1200 800 Pilot Proportion Estimate 0.35 0.73 a) Determine the proportion of the sample to be allocated to each stratum under (1) equal allocation: (11) proportional allocation; () Neyman allocation. b) Suppose the overall sample size is 500. Determine the subsample size in each of the strata under each of the three allocation methods. C) Estimate the variance of the proportion estimator under each of the three allocation methods, as well as under SRS. Which method appears to be best? d) Suppose that a sample of size 300 is drawn under Neyman allocation. The sample proportions in the two strata are respectively 0.24 and 0.71. Determine (t) the overall proportion estimate. (lt) an improved estimate of the variance of the proportion estimator, and (lit) a 95% confidence interval for the population proportion. Question 1 A fitness instructor wants to estimate the mean resting heart rate (measured in beats per minute, BPM) of all members of a gym. She decides to do a fitness test with a stratified random sample of members, with stratum being age group (20-30, 30-40, 40-50, 50 - 60). Based on a pilot study, initial estimates are obtained for the standard deviation of resting heart rate within each age group. Age Group Stratum No. 20 - 30 1 30 - 40 2 40 - 50 3 50 - 60 4 Stratum Population Size 752 950 686 420 Pilot S.D. Estimate 6.3 9.5 4.6 10.5 a) Determine the proportion of the sample to be allocated to each of the three allocation methods. b) Suppose the overall sample size is 450. Determine the subsample size in each of the strata under each of the three allocation methods. c) Estimate the variance of the mean estimator under each allocation scheme and thus identify the optimal method d) Suppose that a sample of size 450 is drawn under proportional allocation. The sample mean for "30 - 40" strata is 5.45. Determine a 95% confidence interval for the population mean